Application de l’Algorithmique Génétique
à l’Analyse Terminologique
Vincent Rialle®, Jean-Guy Meunier©, Ismaïl Biskri©,
Sofiane Oussedikß, Georges Nault©
® Laboratoire TIMC-IMAG, UMR CNRS 5525
Faculté de Médecine, 38706 La Tronche Cedex 9 (Vincent.Rialle@imag.fr)
© Laboratoire d'analyse cognitive de l'information (LANCI). Université du Québec à Montréal
ß Centre de Mathématiques Appliquées de l’Ecole Polytechnique de Paris
Abstract
Computer Assisted Reading and Analysis of Text (CARAT) is the computer technology that offers readers an asssistance in attaining some aspects of the informational or semiotic content of a text. Among all the operations at work in each of these processing, we will study more particularly the classification process. An overall state of the art presentation introduces the various approches to automatic text analysis. Our purpose is mainly to show how the Genetic Algorithm approach to classification can be applied to the problem of semiotic interpretation of text, and most of all in the context of CARAT technology. In this paper, we propose a modeling, by means of a genetic algorithm, of the classification moment of two specific processing flows : the first flow aims at giving the reader hints on the semantics contexts of particular words ; the second flow aims at automatically suggesting hypertext links among segments of texts. So, the main concepts that define GAs will be translated in the terms of classifying segments of texts. This theoretic exposé will be followed by a presentation of some experimental results.
1. Introduction
La Lecture et Analyse de Texte Assistées par Ordinateur (LATAO) a pour objet le traitement automatique du corpus textuel électronique. Elle est aujourd'hui confrontée à des problèmes d'ampleur (autoroute électronique, CD-ROM, popularisation des micro-ordinateurs, course à la performance technologique), de plasticité (adaptation à de nouveaux besoins) et de polyvalence (augmentation de la variété des utilisateurs).
Dans une perspective de LATAO, le rappel ou l’extraction automatique d'information, correspondant au concept actuel de data-mining, constitue une première étape d'un processus de lecture et d'analyse d'un texte. Dans la présente recherche, nous proposons une modélisation particulière du concept de LATAO par l'Algorithmique Génétique (AG).
2. L'Algorithmique Génétique
2.1 Présentation générale
L'algorithmique génétique offre une solution originale au problème fondamental de la classification automatique (Rialle, 1996). La notion d’algorithme génétique, introduite par John H. Holland (1975, 1992), a été considérablement développée au cours des années 80 (Goldberg, 1989, 1994 ; Davis, 1991 ; Rawlins, 1991 ; Varela et Bourgine, 1992 ; Michalewicz, 1994). Le principe en est simple et repose sur :
- un codage des informations, situations, problèmes et solutions, sous la forme de chaînes d'éléments de base insécables (building blocks) ;
- une faculté de reproduction en grand nombre de telles chaînes ;
- l'existence d'une fonction d'adéquation (ou fonction d'adaptation) permettant de d'évaluer la qualité de chacune des chaînes créée par l'algorithme.
Plusieurs applications de l'algorithmique génétique à la construction de classifieurs ont déjà été expérimentées avec succès, à commencer par les travaux de celui qui en est le premier promoteur, J. Holland. Depuis quelques années se développe une branche à part entière de l’apprentissage automatique de connaissances fondée sur l’utilisation des AGs, et connue sous le terme anglais de Genetic Based Machine Learning Algorithms (e.g., Green et Smith, 1993 ; Venturini, 1994 ; Oussedik et Rialle, 1997).
2.2 Cycle de base et présentation formelle de l'AG
On peut présenter de manière synthétique le fonctionnement de l'algorithme génétique par le cycle suivant :
Ce cycle est le plus classique (Goldberg, 1989) et connaît diverses variantes selon l'application que l'on traite.
Soit
: population initiale d’individus créée aléatoirement
p : entier naturel : nombre d’individus de la population ;
n : entier naturel : nombre de caractères (ou gènes) des éléments de la population (i.e., longueur de la représentation génique).
représentant la population des solution potentielles au tème cycle de l’AG, voici d’une manière plus détaillée les étapes du cycle de base :
SÉLECTION : on effectue, dans Pt, p tirages aléatoires avec remise, selon la distribution de probabilité définie par Probs, ce qui revient à sélectionner prioritairement les éléments les plus performants. Afin de préparer l'étape suivante, ces éléments sont rangés par couples au fur et à mesure du tirage.
REMPLACEMENT : on forme l'ensemble U = Pt u P't et l'on ordonne les éléments de U du plus au moins performant selon le critère ƒ. On construit ensuite la nouvelle population Pt+1 en prenant soit les p plus performants éléments de U (taille de la population fixe), soit en éliminant les éléments les moins performants selon un critère de suppression propre à l'application (taille de la population variable).2.3 Les opérateurs génétiques
Les principaux opérateurs génétiques sont le croisement et la mutation. D'autres opérateurs, moins courants, existent ou peuvent être conçus. Ils sont spécifiques à des domaines ou des applications particulières (voir les ouvrages de références).
2.3.1 Le croisement
Le croisement (anglais : crossing-over), ou opérateur de recombinaison, est souvent le premier opérateur génétique appliqué au cours d'un cycle (il correspond au phénomène de translocation réciproque en génétique, responsable de diverses maladies chromosomiques). Il porte sur les paires d'individus issues de l'étapes de sélection et consiste en l'échange de parties de chromosomes comme indiqué sur la figure 1. Les parties de chacun des chromosomes sont en général déterminées par un même point de rupture. Pour un chromosome, la partie située au-delà du point de rupture est échangée avec la partie homologue de l'autre.
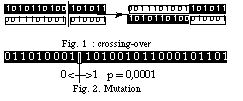
NB. Il existe des croisements à points de rupture multiples, dans lesquels plusieurs segments de gènes peuvent être interchangés entre deux chromosomes.
2.3.2 La mutation
La mutation est tout d’abord la sélection au hasard de l'un des bits du chromosome, suivie du changement de sa valeur avec une probabilité prédéfinie, dite probabilité de mutation (Fig. 2). Par exemple, si la probabilité de mutation est 0,0001, le bit du chromosome tiré au hasard aura une chance sur 10 000 de devenir 0 s'il est à 1 ou de devenir 1 s'il est à 0.
La mutation seule ne saurait garantir la progression vers une solution dans des délais raisonnables. Elle constitue cependant un générateur de diversité qui prémunit contre la stagnation de la population, c'est-à-dire contre la formation d'une population de solutions "coincée" dans un sous-domaine de possibilités et incapable d'évolution. Une telle population correspond à un minimum local de la fonction d'adaptation (dont la méthode du recuit-simulé par exemple constitue l'un des moyens pour en sortir, dans le cas de certains algorithmes non-génétiques). Le croisement et la mutation permettent donc de créer de nouvelles chaînes chromosomales à partir d'anciennes, parmi lesquelles certaines devraient statistiquement avoir de meilleures propriétés que celles dont elles sont issues
3. Algorithmes Génétique et LATAO
3.1 L'objectif de modélisation
Nous proposons, dans cette dernière partie de l'article, un travail de modélisation de l'approche LATAO dans les termes de l'Algorithmique Génétique. Les principaux concepts définissant l'AG vont ainsi être traduits en terme de traitement textuel. Cette modélisation a de plus été confirmée par quelques expérimentations concrètes sur des textes. Nous présenterons donc, à la suite de l'exposé théorique, quelques-un des premiers résultats.
Dans la perspective LATAO, l'algorithme génétique consiste à chercher, parmi les différents segments d'un texte, des structures régulières ou des classes de régularités. L’AG est vu comme un processus de traitement classificatoire qui identifie des segments de textes contenant un "même" type d'informations. L'analyse de texte est conçue comme résultant d'une opération de classification de segments de texte fondée sur un critère de ressemblance ou d'équivalence.
Ces segments d'information sont le plus souvent des pages ; ces pages étant constituée d'unifs (pour unité d'information). Une unif représente toute unité d'information susceptible d'une analyse. Dans notre cas, les unifs pourront être des mots, simples ou composés, des lexèmes, etc. La détermination des unifs et des segments est réalisée à l'aide de logiciels d'analyse de texte par ordinateur tels que SATO, BOOKMANAGER, SPIRIT, OPEN TEXTE, NATUREL, etc., et donne lieu à un lexique. Vient ensuite une étape de marquage linguistique sur ce lexique, tel qu’un marquage morphologique, (e.g., [porte]nom vs [porte]verbe), ou encore un marquage de mots composés (e.g., [porte d'entrée]). De tels marquages sont réalisés au moyen de logiciels spécialisés tels que Tact, X-TRACT, ALceste, SATO, Termino, XEROX, etc. Le texte original est alors transformé en un ensemble de segments contenant uniquement un choix contrôlé et pondéré d'unités d'informations.
On détermine, pour chaque unif, sa présence ou absence dans chaque segment, afin de parvenir à une représentation vectorielle et matricielle. Chaque segment peut alors être représenté par un vecteur d'unifs dans lequel la ième position du vecteur indique la présence (1) ou l’absence (0) de l’unif n° i dans le segment. Ces vecteurs sont ensuite assemblés pour former une matrice segments-unifs de taille (n ¥ m), c’est-à-dire de n segments par m unifs (tableau 1).
3.2 La classification génétique
L'objectif de la modélisation est regrouper de manière optimale des segments dans des classes de segments, appélées plus simplement classes. L'affectation de segments à des classes s'appelle un classement, tandis que le processus de recherche du meilleur classement est une classification. Dans la suite de l'article, nous réserverons donc le terme de classification automatique au processus complet de recherche du meilleur classement.
La matrice (segments ¥ unifs), précédemment définie, sera utilisée par la fonction d’adaptation, définie plus loin, pour calculer des degrés d’affinité entre segments pouvant justifier leur association en classes. Une classe sera donc un ensemble de segments peu distants au sens d'une mesure d’affinité donnée par la fonction d'adaptation, la signification de chaque classe revenant à l'utilisateur.
Étant donné que les vecteurs de la population initiale représentent des solutions potentielles au problème de recherche du meilleur classement, l'AG aura pour tâche d'effectuer sur ces vecteurs initiaux un grand nombre de modifications, réorganisations, mutations, pour tenter de produire le meilleur (au sens de la fonction d'adaptation) vecteur de solution potentielle (ou les principaux meilleur vecteurs). Les vecteurs produits par l’AG sont des tentatives de modèles de classement, c’est-à-dire des tentatives d’attribution de chaque segment du texte à une classe unique. C’est pourquoi nous les appellerons des classifieurs.
La population initiale de classifieurs est construite de manière entièrement aléatoire. A l'initialisation de l'AG, le nombre de classes est arbitrairement choisi assez grand : nous avons utilisé comme nombre initial de classes, noté NBC, le nombre n de segments du texte, de manière à donner au processus la liberté de construire autant de classes de segments que possible. Il y aura donc toujours NBC classes potentielles, mais un certain nombre d’entre elles, que l’on souhaite le plus grand possible, seront vides. C'est tout le sens de la fonction d'adaptation que de réduire le nombre de classes effectives à une valeur optimale au cours des cycles de l'AG. Le nombre de cycle de l'AG est également arbitrairement fixé à une valeur assez grande, de l'ordre de mille cycles.
3.3 Définition ensembliste et population initiale de classifieurs
L’introduction du concept de population de classifieurs et en particulier de population initiale de classifieurs dans le contexte LATAO, passe par la définition préalable des trois ensembles suivants :
a) l'ensemble T des n segments du texte. Soit T = {S1,..., Sn}
b) L'ensemble K des NBC classes. Soit K = {C1,..., CNbC}, NbC représentant le nombre maximum de classes, fixé à l’initialisation. L’un des effets de la recherche génétique sera de distribuer les segments parmi un nombre réduit de ces classes, et de laisser les autres vides.
c) L'ensemble des classifieurs, ou population des classifieurs, P. Un classifieur (ou chromosome, selon la métaphore génétique) est un vecteur de dimension n (nombre de segments) dont la position n° i correspond au iéme segment du texte original. Cette position contient un entier indiquant la classe à laquelle l’algorithme propose d’affecter ce segment. Un classifieur code donc une suggestion de classement de la suite des segments de texte.
L'ensemble P contient un nombre p constant de classifieurs fixé à l'initialisation de l'algorithme.
Le i ème classifieur de la population correspond au vecteur Vi = (i1, ..., ij, ..., in), Cij Œ K.
Un classifieur représente une fonction projetant l'ensemble T des segments du texte dans l'ensemble K des classes. Ce type de codage oblige un segment à ne se retrouver que dans une seule classe.
Exemple : T = {S1, S2, S3, S4 } ; K = {C1, C2, C3}, exemple de vecteur : V = (2,1,3,2).
Interprétation : le 1er segment appartient à la classe C2, le 2ème à C1, le 3ème à C3 et le dernier à C2.
La population initiale est obtenue par une génération aléatoire de p vecteurs classifieurs tels que définis précédemment.
3.4 La Fonction d'Adaptation
3.4.1 Finalité
La fonction d'adaptation à pour but d’évaluer les classifieurs et d’orienter l’ensemble de la recherche génétique vers le "meilleur" d’entre eux. C'est une fonction définie sur l'ensemble des classifieurs et à valeur réelle.
Une classement idéal est un classement dans lequel tous les segments ont une valeur d’affinité maximale, selon un critère d’affinité particulier, défini plus loin. Pour un tel classement idéal, le fait de déplacer un segment d'une classe à une autre (par mutation ou croisement), ne pourra que diminuer la qualité du classement, c'est-à-dire la valeur de la fonction d'adaptation du classifieur correspondant.
Les classifieurs retenus pour les opérations de reproduction seront donc ceux qui possèdent les meilleures valeurs par la fonction d'adaptation. Tout l’art du modélisateur va donc être de trouver la fonction d'adaptation la plus à même de conduire l'AG vers la meilleure solution.
La fonction d'adaptation doit être la plus discriminante possible. Ce caractère discriminant porte sur deux aspects complémentaires :
- la cohésion interne du classement : c'est le degré d’affinité des segments à l’intérieur de chaque classe ;
- la différenciation du classement : c'est le degré de dissimilarité des classes entre elles.
3.4.2 Choix d'un critère d’affinité
La fonction d'adaptation que nous avons expérimentée est fondée sur un critère d’affinité (nous préférons, dans une application de classification, le terme d’affinité à celui de similitude, quelques fois employé) : le coefficient de Jaccard (Salton, 1989, p. 318). Ce coefficient n'utilise que la présence ou l'absence des unifs dans les segments. Il constitue une mesure courante pour l'évaluation de la similitude de documents dans le cas de la recherche d'information. Il a notamment été utilisé pour l'indexation de documents (Gordon, 1988). Il faut cependant noter qu'il existe d'autres critères d’affinité de segments de textes. Salton (1971, 1975, 1983, 1989) en particulier en propose quelques-uns. Le coefficient de Jaccard a été retenu pour cette première expérimentation en raison de sa rapidité de calcul. Nous prévoyons cependant, dans une prochaine étape, l'utilisation de coefficients plus complexes et la comparaison de leurs performances.
Le coefficient de Jaccard est calculé pour un couple de segments (Xj, Xk). Il est égal à la proportion d'unifs communes aux deux segments (notation : |Xj " Xk|) par rapport aux nombre total d'unifs présents dans les deux segments (|Xj " Xk|). Soit : Aff (Xj, Xk) = |Xj " Xk| / |Xj " Xk|
Les indices utiles pour la fonction d’adaptation sont définis de la façon suivante :
a) la cohésion interne d'une classe Ci est évaluée par un coefficient de cohésion interne noté CI(i). Ce coefficient est la somme pondérée des affinités des segments pris deux à deux dans cette classe. Il est défini par :
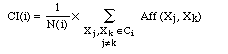
N(i) est le nombre de couples de segments de la classe Ci.
b) la différenciation d'une classe Ci est évalué par le coefficient de dissemblance externe, noté CE(i), calculé pour Ci par rapport à toutes les autres classes. Sa définition est la suivante :
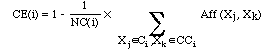
CCi est l'ensemble complémentaire de Ci. Cet ensemble contient tous les segments qui n'appartiennent pas à Ci. NC(i) est le nombre de couples (Xj, Xk), Xj appartenant à Ci et Xk appartenant à CCi.
c) l’indice de qualité d’une classe Ci est la somme des indices de cohésions interne et externe, soit CI(i) + CE(i). Remarque : les indices de qualité des classes vides seront nuls, ceux des classes denses, au sens des coefficients de cohésion interne et externe, seront élevés.
3.4.3 Définition de la fonction d’adaptation
La fonction d'adaptation ƒ proposée est égale à la somme des indices de qualité des classes suggérées par un classifieur. Soit :
3.5 Résultats d'expérimentation
L'expérimentation a porté sur un échantillon textuel du 9ème numéro d'une revue scientifique : Spirale (revue canadienne francophone de littérature, philosophie et art visuels). L'algorithme génétique a été développé sur le logiciel Matlab 4.0 et a été intégré au système Aladin (Seffah et Meunier, 1995), une plate-forme informatique pour l'Analyse de Texte par Ordinateur en cours de développement au LANCI. Les tests ont été effectués sur un PC Pentium, 150 Mhz.
Initialisation de l'algorithme : A l'initialisation, le nombre de classes de départ (NbC) est égal au nombre de segments. La probabilité de croisement a été fixé à 0,8, et celle de mutation à 0,05. Le nombre de classifieurs dans la population initiale était de 100. Le nombre de générations (ou itérations) de l'algorithme était de 300.
La matrice texte : Le texte a été partitionné uniformément en 54 segments de 50 mots chacun, la fin d'un segment est déterminé de la façon suivante : on compte 50 mots après le début du segment, et on ajoute à ces 50 mots les mots restant jusqu'au point suivant.
On disposait au départ d'un lexique composé de 1701 mots dont le nombre s'est restreint à 1360 racines après un traitement préliminaire de lemmatisation. La matrice texte est une matrice de type (nombre d'unifs ƒ nombre de segments). Elle était donc de dimension (1360 % 54), indiquant pour chaque unif, sa présence ou son absence dans chaque segment de texte.
Résultats : La classification obtenue montre que : 1) le nombre de classes est passé de 54 à 24 à la fin du processus de classification ; 2) le contenu des classes est le plus souvent interprétable par l'utilisateur, e.g., la classe 4 contient les segments 8 et 21, montrés ci-dessous :
Segment 8 : "Enfin, Joëlle Delattre aborde le problème des livres pour enfants aveugles et malvoyants, dont certains éditeurs semblent d'ailleurs se préoccuper en proposant maintenant des albums spécialement conçus pour eux. comme on le voit, une certaine diversité caractérise cette livraison, mais son unité nous semble résider dans la prudence des approches : La littérature de jeunesse ne représente ni toute la lecture ni toute la littérature, mais elle existe, avec un présent et un passé suffisamment riches."
Segment 21 : "Se pose alors, à l'enseignant convaincu de l'importance de la lecture littéraire, la question du choix des textes et des modalités de transmission. En effet, il n'y a à ce niveau ni propositions ministérielles de listes d'ouvrages, comme le collège ; ni tradition d'enseignement universitaire spécialisé pour définir de méthodes ; la formation initiale et continue est disparate, largement laissée à l'initiative de chacun. En fait, l'instituteur, qui choisit ses textes et ses démarches, sciemment ou non, met en jeu toute sa conception personnelle de la culture et du rôle de l'école dans la formation de l'enfant."
On retrouve dans ces deux segments les unifs (soulignées) qui les associent à la même classe, soit {enfant, littérature, lecture}.
Une analyse plus approfondie des résultats requiert ensuite l'intervention du linguiste, du terminologue ou du spécialiste du domaine. Cette intervention est indispensable aussi bien au moment de la préparation de la matrice texte qu'à celui de l'analyse des résultats.
4. Conclusion
L'utilisation de l'algorithmique génétique que nous appliquons à l'analyse de texte en est encore au stade de l'observation expérimentale. Mais c'est cependant un territoire très prometteur et très flexible, qui mêle le codage, le traitement des données, le calcul des probabilités, l'I.A et le mode génétique de l'évolution.
Les perspectives de recherche se situent autour de l'étude plus approfondie de l'algorithme génétique appliqué au LATAO et de la comparaison des résultats obtenus avec ceux d'autres systèmes classifieurs que nous développons actuellement, tels le recuit simulé et le réseau de neurones ART.
Remerciements
Le présent travail a été réalisé dans le cadre du projet franco-québécois "Les classifieurs émergentistes et le traitement de l’information" sous la tutelle, pour ce qui concerne la France, du Ministère de l'Enseignement Supérieur et de la Recherche (M.E.N.E.S.R.I.P., Délégation à L’information Scientifique et Technique, programme "Ingénierie linguistique et de la connaissance") et Ministère des Affaires Étrangères, et pour ce qui concerne le Québec : Gouvernement du Québec - Ministère des relations Internationales. Nous tenons à vivement remercier ces tutelles pour le travail de coopération qu'elles ont permis. Nous remercions également l'ensemble de l'équipe du LANCI et tout particulièrement M. Nyongwa et I. Biskri pour leurs conseils et support technique.
Références
Bersini, H. et Varela, F.J. (1991). Hints for adaptive problem solving gleaned from immune networks. In Schwefel P. et Männer R. (éd.) Parallel Problem Solving From Nature, Lecture Notes in Computer Science n° 496, Berlin : Springer-Verlag, 343-354.
Davis, L. (1991). Handbook of Genetic Algorithms, New York : Van Nostrand Reinhold.
Dehaene, S. et Changeux, J.P. (1989). A simple Model of Prefrontal Cortex Function in Delayed-Response Tasks, Journal of Cognitive Neuroscience, 1, 3, 244-261.
Goldberg, D.E. (1989). Genetic algorithms in search, optimisation and machine learning. Reading, MA : Addison-Wesley.
Gordon (1988). Probabilistic and genetic algorithms for document retrieval. Communications of the ACM, 31(10) : 1208-1218.
Greene, D.P., Smith S.F. (1993). Competition-Based Induction of Decision Models from Examples. Machine Learning vol. 13, 229-57.
Hoffmeister, F. et Bäck, T. (1992). Genetic Self-Learning. In Varela F.J. et Bourgine P. (éd.) Toward a Practice of Autonomous Systems. Cambridge, MA : MIT Press, 227-235.
Holland, J. (1975). Adaptation in Natural and Artifial Systems, University of Michigan Press. Ann Arbor, Michigan.
Holland, J. (1992). Genetic Algorithms, Scientific American, July, pp. 66-72. Tr. Fr. : Les algorithmes génétiques, Pour la science, 179, 44-50.
Michalewicz, Z. (1994). Genetic Algorithms + Data Structures = Evolution Programs. Berlin : Springer-Verlag.
Mitchell, T. (1997). Machine Learning. New York : McGraw Hill.
Oussedik, S. et Rialle, V. (1997). AGADE, a GBML System using two Fitness Functions : Theoretical, experimental, and comparative study. EA’97, Third Int. Conf. on Evolutionary Computation, Nimes, 21-24 october.
Rawlins, G.J.E. (éd.) (1991). Foundations of Genetic Algorithms., San Mateo, CA : Morgan Kaufmann.
Rialle, V. (1995). Vers la maîtrise informatique de la connaissance. In : Dr H. Joly (éd.), Biomédecine 2000, Paris : Lavoisier. 52-75.
Rialle (1996). Cours d’Intelligence Artificielle du DEA de Sciences Cognitives. Institut National Polytechnique de Grenoble.
Salton, G. (1971). The SMART retrieval system : Experiments in Automatic Document Processin. Englewood Cliffs, N.J. : Prentice-Hall.
Salton, G. (1975). Dynamic Information and Library Processing. Englewood Cliffs, N.J. : Prentice-Hall.
Salton, G. et McGill, M. (1983). Introduction to models of Information Retrieval, New York : Mc Graw Hill.
Salton, G. (1989). Automatic Text Processing : The transformation, Analysis and Retrieval of Information by Computer. Reading, MA : Addison Wesley.
Salton, G. et Buckley, A.C. (1994). Automatic structuring and retrieval of large text file. Com. of the ACM, 37(2), 97-107.
Seffah, A. et Meunier, J.G. (1995). ALADIN : Un Atelier génie logiciel orienté objets pour l'analyse cognitive de textes. In Bolasco S., Lebart L. et Salem A. Analisti Statistica dei Dati Testuali. JADT, 1995, Rome : CISU, (2), 105 -113.
Varela, F.J. et Bourgine, P. (éd.) (1992). Toward a Practice of Autonomous Systems. Proc. 1st Europ Conf Artificial Life, Cambridge, MA : MIT Press.
Venturini, G. (1994). Characterizing the Adaptation Abilities of a Class of Genetic Based Machine Learning Algorithms. In Varela F.J. et Bourgine P. (éd.) (1992). Toward a Practice of Autonomous Systems (Proc. 1st Europ Conf Artificial Life), Cambridge, MA : MIT Press, 302-309.
Virbel, J. (1993). Reading and Managing Texts on the Bibliothèque de France Station. In P. Delany et G. Landow (Ed.), The Digital Word : Text Based Computing in the Humanities. Cambridge, MA : MIT Press.