Sommaire des JADT 1998
LES CHAMPS DE MARKOV DANS L’ANALYSE DE TEXTE ASSISTÉE PAR ORDINATEUR. MODÉLISATION ET PREMIERS RÉSULTATS.
Lakhdar Remaki, Jean Guy Meunier, Sâad Hamidi.
Laboratoire d’Analyse Cognitive de l’Information (LANCI)
Université du Québec à Montréal.
Case postale 8888, succursale centre-ville
Montréale (Québec) Canada, H3C 3P8
Abstract
First results obtained by a Markov Random Fields (MRF) model applied to an automatic information retrieval in full text document, are investigated and discussed. We use a document composed from merge between a text of SPIRALE review and few pages of Hydro-Quebec text, which don’t share the same semantics. Our aim is to observe the MRF behaviour with respect to the Hydro-Quebec text in the full text, by classification or by a flow of queries. The results show that the MRF model is able to identify the Hydro-Quebec text with a good precision after classification process or a queries flow process, and it can do more, it can identify a noise caused by a user in a query.
1. Introduction
Comment, dans les stratégies d'accès au contenu de l'information d'un texte électronique, tenir compte simultanément de la constante modification du corpus et de l'interaction avec un utilisateur en situation d'analyse. Le premier aspect touche la plasticité du traitement, le second sa dynamicité. Plusieurs solutions ont été proposées pour aborder ces questions, à travers les modèles statistiques classificatoires[Croft,1980; Diday,1987; etc...], multidimensionnels [Cheesemann et al., 1988; Lebart and Salem, 1994 ; etc...]. Bien que systématiques et efficaces, la plupart de ces modèles demeurent cependant statiques dans leur traitement ; ils exigent la reprise du calcul à chaque modification du corpus. Les modèles connexionnistes [Veronis, 1990 ; Salton et al., 1994; Meunier, Nault et Lelu, 1996 etc...] semblaient sensibles à ces dimensions du fait de leur propriété d’incrémentalité, mais ne peuvent traiter efficacement la plasticité et encore moins l'interaction dynamique. Les modèles algorithmes génétiques appliqués au texte [Rialle, Oussedik, et Meunier, 1997 etc...] se focalisent sur la dimension plastique mais ne touchent pas l'interaction dynamique. Le modèle dit "champs de Markov ≤ offre une solution intéressante. Très utilisé dans la reconnaissance et la restauration d’images [Geman and Geman, 1984; Chellapa, 1991 ; etc...], ce modèle semble pouvoir résoudre les deux problèmes cités ci-dessus. Pour réaliser un tel modèle, il faut d’abord soumettre le texte à une analyse morpho-syntaxique qui permet le calcul d’une distance entre énoncés [Pêcheux, 1969; DelVigna, 1977; Rouault, 1994], ensuite réaliser une analyse linguistique classique basée sur des poids assignés à des unités d’informations, en générale des mots. Le texte est découpé en segments qui seront considérés comme une famille stochastique, et formeront ainsi un champ de Markov. Par ce biais, l’aspect dynamique, est mathématiquement modélisé par l’influence mutuelle de la requête et du processus de filtration généré par l’algorithme connu sous le nom de Gibbs sampler[Geman and Geman, 1984]. La dimension plastique est assurée par la topologie facilement modifiable de la représentation. En conséquence, le modèle n’est affecté ni par la taille du corpus ni par sa modification constante. Bouchaffra et Meunier [1995, 1996] ont proposé des variantes de ces modèles pour l'analyse thématique et la requête d'information sur de grands corpus. Dans ce papier, nous présentons les premiers résultats d'application d'un modèle "champs de Markov" à un corpus échantillon. Nous essayons de valider par la pratique, les concepts théoriques du modèle. Le corpus choisi est un mélange d’un texte de la revue SPIRALE en sciences de l’éducation et une partie d’un texte de l’Hydro-Quebec qui jouera le rôle d’un bruit. Un grand intérêt sera porté au comportement du modèle vis à vis de ce bruit.
2. Calcul des paramètres associés à la distribution de Gibbs et mise en œuvre de la méthode
Le texte est décomposé en segments de 32 lignes. Ces segments seront considérés comme des réalisations d’une famille de variables aléatoires X={ Xi , 1£i£k} identifiée à un champ de Markov. Les détails de l’aspect théorique de ce modèle sont illustrés dans [Bouchaffra et Meunier ,1995, 1996]. Le paramètre le plus pertinent et le plus difficile à estimer est l’énergie U du système, ce qui revient à estimer les potentiels des cliques Vc(x) [Hammersley and Clifford 1971]. Griffeat, Kindermann and Snell [Griffeat 1976 ; Kindermann and Snell 1980] ont montré l’existence d’une forme canonique unique de ces potentiels, donnée par la formule suivante :
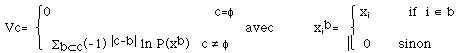 ici f est l’ensemble vide, |c-b| le cardinal de l’ensemble c-b où c et b deux cliques données, P la loi de probabilité associée au Champ de Gibbs. Cette formule suppose connue la loi de probabilité P, ce qui n’est pas le cas, mais elle peut être exploitée dans une perspective de prédiction correction : c’est-à-dire que nous approchons cette loi par une loi gaussienne de caractéristiques m et s que nous déterminons empiriquement. Nous utilisons ensuite celle-ci pour calculer les potentiels par la formule ci-dessus. L’image dégradée Y = f(H(X)) + N sera calculée, en prenant la fonction radicale pour la fonction de transformation f, l’identité pour H et le bruit N sera considéré gaussien ; les meilleurs résultats sont obtenus par un m calculé à partir de la moyenne des segments. Ainsi nous pouvons mettre en œuvre l’algorithme de Gibbs (expliqué en détail dans [Geman and Geman, 1984]) qui permet de maximiser la probabilité conditionnelle p(X=x /Y=y), où Y est la configuration dégradée observée à l’état initial t = 0, et X est la nouvelle configuration probable à l’instant t. La température T est laissée constante et égale à un.
ici f est l’ensemble vide, |c-b| le cardinal de l’ensemble c-b où c et b deux cliques données, P la loi de probabilité associée au Champ de Gibbs. Cette formule suppose connue la loi de probabilité P, ce qui n’est pas le cas, mais elle peut être exploitée dans une perspective de prédiction correction : c’est-à-dire que nous approchons cette loi par une loi gaussienne de caractéristiques m et s que nous déterminons empiriquement. Nous utilisons ensuite celle-ci pour calculer les potentiels par la formule ci-dessus. L’image dégradée Y = f(H(X)) + N sera calculée, en prenant la fonction radicale pour la fonction de transformation f, l’identité pour H et le bruit N sera considéré gaussien ; les meilleurs résultats sont obtenus par un m calculé à partir de la moyenne des segments. Ainsi nous pouvons mettre en œuvre l’algorithme de Gibbs (expliqué en détail dans [Geman and Geman, 1984]) qui permet de maximiser la probabilité conditionnelle p(X=x /Y=y), où Y est la configuration dégradée observée à l’état initial t = 0, et X est la nouvelle configuration probable à l’instant t. La température T est laissée constante et égale à un.
3. Le schéma expérimental
Nous avons utilisé une partie d’un texte de la revue SPIRALE dans laquelle nous avons inséré quelques pages d’un texte d’Hydro-Québec (segments 42, 43, 44, et 45.), et notre attention s’est portée sur le comportement du modèle MRF par rapport à cette partie insérée. Dans les segments 42 et 45 les deux textes, Hydro-Québec et SPIRALE se chevauchent. Nous avons utilisé une distance euclidienne pour la détermination du système de voisinage. Cette distance est calculée après une représentation matricielle du texte, dont les lignes représentent les différents segments, et les colonnes les différentes unités d’informations (UNIFS), lesquelles sont dans notre cas des Quadri-Grams. Les différentes composantes de la matrice désignent le nombre d’occurrences de l’UNIF dans chaque segment. Nous renvoyons le lecteur non familiarisé avec la technique de traitement de texte par les N-Grams (pour nous N=4) à [Kimbrell, 1988].
4. Résultats
∑
Test 1 : Classification ; nous avons obtenu sept classes dont voici celles où apparaît le texte d’Hydro-Quebec: C11{40,41,42,54}, C12{43,44,45}.
∑
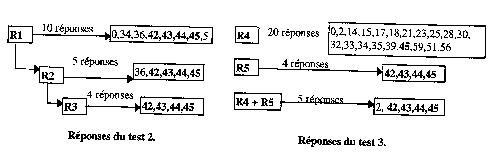
Test 2 : Interrogation du texte par un flux de requêtes R1, R2, R3 (R1 : autochtone, R2 : convention (premier raffinement), R3 : territoires du nord (deuxième raffinement))
∑
Test 3 : Interrogation du texte avec concaténation de requêtes (R4 : littérature, R5 : autochtones et convention des territoires du nord).
5. Commentaires et conclusion
∑
Test 1 : Le classifieur a pu isoler les segments 43, 44 et 45 (texte d’Hydro-Québec) dans une classe a part (classe C12). Le segment 42 apparaît dans la classe 11, ce qui peut s’expliquer par le chevauchement des deux textes cité plus haut.
∑
Test 2 : La partie du texte d’Hydro-Québec qui traite d’une convention sur les territoires des autochtones du nord, a pu être complètement identifiée par le classifieur après trois requêtes successives (R1, R2, R3), ce qui montre que le modèle permet une bonne interaction avec l’utilisateur.
∑
Test 3 : Le but du troisième test, et de savoir si le modèle n’agit pas d’une façon booléenne, c’est à dire s’il ne va pas chercher toutes les parties du texte, où apparaissent les mots composants la requête. Pour cela nous avons interrogé le texte d’abord par le mots littérature (R4), car la partie du texte SPIRALE que nous avons utilisée est focalisée autour du thème de la littérature de jeunesse. La réponse était de 20 segments. La requête R5 composée de mots clefs du texte d’Hydro-Québec nous a permit d’isoler(comme dans le test 2) le texte d’Hydro-Québec. Nous avons interrogé ensuite le texte par une requête(R4 + R5), R4 joue le rôle de bruit par rapport à R5 dont le contenu sémantique est plus riche. Si le modèle agit d’une façon booléenne, nous aurions eu comme réponse les 20 segments de R4 plus les 4 de R5, or nous avons obtenu les 4 segments de R5 et un seul des 20 segments de R4 (le segment 2). Nous pouvons ainsi conclure que le modèle a pu identifier R4 comme étant un bruit causé par l’utilisateur dans la requête R4 + R5.
Références
Bouchaffra, D et Meunier, J. G. (1996). A Thematic Knowledge Extraction Modelling through a Markovian Random Fields Approach, DEXA database and Expert Systems applications. N.Rewell & Min Tjoa (ed) p 329-339.
Bouchaffra, D et Meunier, J. G. (1985). A Markovian Random Field Approch to information Retrieval, international Conference On Document Analysis and Recognition ICDAR vol 11 p 997-1002,
Cheeseman .P, Self .M, Kelly .J, Stutz .J, Taylor .W and Freeman .D. (1988).Baysian classification. Proceeding of AAAI, Minneapolis, 607-611.
Chellappa, R., Jain, A. (1991). Markov random fields : theory and application. Academic Press, INC.
Croft, W. B. (1980). A model of cluster searching based on classification. Information Systems,189-195.
Diday, E. (1987). Orders and overlapping clusters by pyramids. Rapport de recherche n 730, INRIA.
Geman, S. and Geman, D. (1984). Stochastic relaxation, Gidds distribution and the Bayesian restoration of image. IEEE Transaction on Pattern Analysis and Machine Intelligence, 6(6) :721-741,
Griffeat, D. (1976). Introduction to random fields. In Kemeny, J. G., Snell, J. L., and Knapp, A. W., editors, Denumerable Markov Chains, Chapter 12, pages 425-458. Springer-Verlag, New York, 2nd edition.
Hammersley, J.M.and Clifford, P. Markov field on finite graphs and lattices. Unpublished.
Kimbell, R. E. (1988). Searching for text ? Send an N-Grams !. Byte, 297-312.
Kindermann, R. and Snell, J.(1980). Markov fields and their application. Amer.Math.Soc, Providence,R.I.
Lebart, L and Salem, A. (1994). Statistique textuelle. Paris: Dunod.
Pêcheux, M. (1964). Analyse automatique du discours , Dunod.
Rouault, J. (1994). Analyse automatique du discours : Note sur le système 3AD75, Communication interne, Université Stendhal, Grenoble.
Salton, G. , Allan, J., & Buckley, C. (1994). Automatic Stucturing and Retrieval of Large Text File. Communications of the ACM 37 (2), 97-107.
Veronnis, J., Ide, N. M., & Harie , S. (1990). Utilisation de grands réseaux de neurones comme modèles de représentatons sémantiques. Neuronimes,
Vincent, R. Meunier, J.G, Oussedik, S, Nault, G. (1997). Semiotics and Modeling Computer Classification of Text with Genetic Algorithm : Analyse and first Results. ISAS’97, 325-330.
Sommaire des JADT 1998
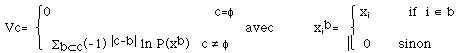 ici f est l’ensemble vide, |c-b| le cardinal de l’ensemble c-b où c et b deux cliques données, P la loi de probabilité associée au Champ de Gibbs. Cette formule suppose connue la loi de probabilité P, ce qui n’est pas le cas, mais elle peut être exploitée dans une perspective de prédiction correction : c’est-à-dire que nous approchons cette loi par une loi gaussienne de caractéristiques m et s que nous déterminons empiriquement. Nous utilisons ensuite celle-ci pour calculer les potentiels par la formule ci-dessus. L’image dégradée Y = f(H(X)) + N sera calculée, en prenant la fonction radicale pour la fonction de transformation f, l’identité pour H et le bruit N sera considéré gaussien ; les meilleurs résultats sont obtenus par un m calculé à partir de la moyenne des segments. Ainsi nous pouvons mettre en œuvre l’algorithme de Gibbs (expliqué en détail dans [Geman and Geman, 1984]) qui permet de maximiser la probabilité conditionnelle p(X=x /Y=y), où Y est la configuration dégradée observée à l’état initial t = 0, et X est la nouvelle configuration probable à l’instant t. La température T est laissée constante et égale à un.
ici f est l’ensemble vide, |c-b| le cardinal de l’ensemble c-b où c et b deux cliques données, P la loi de probabilité associée au Champ de Gibbs. Cette formule suppose connue la loi de probabilité P, ce qui n’est pas le cas, mais elle peut être exploitée dans une perspective de prédiction correction : c’est-à-dire que nous approchons cette loi par une loi gaussienne de caractéristiques m et s que nous déterminons empiriquement. Nous utilisons ensuite celle-ci pour calculer les potentiels par la formule ci-dessus. L’image dégradée Y = f(H(X)) + N sera calculée, en prenant la fonction radicale pour la fonction de transformation f, l’identité pour H et le bruit N sera considéré gaussien ; les meilleurs résultats sont obtenus par un m calculé à partir de la moyenne des segments. Ainsi nous pouvons mettre en œuvre l’algorithme de Gibbs (expliqué en détail dans [Geman and Geman, 1984]) qui permet de maximiser la probabilité conditionnelle p(X=x /Y=y), où Y est la configuration dégradée observée à l’état initial t = 0, et X est la nouvelle configuration probable à l’instant t. La température T est laissée constante et égale à un. 