Représenter les données textuelles par les arbres...
|
Jean Pierre Barthélemy Dépt Intelligence Artificielle et Sciences Cognitives ENST Bretagne* |
Xuan Luong Bases, Corpus et Langage UPRESA 6039 CNRS - INaLF Université de Nice** |

Abstract
This paper discusses the use of trees arising from phylogenetic reconstruction applied to the analysis of textual data. The subject is introduced, in a non formal way, from data describing the lexicon associated with Giraudoux’s works. Then the model is formally described, including algorithmic aspects. The last section is devoted to applications to textual data of various kind: grammatical categories (Lob corpus), most frequent words within a corpus (Shakespeare) and use of punctuation marks (Zola).
Introduction
L'analyse des données (textuelles ou autres) n'a certes pas inventé la notion de représentation arborée. Celle-ci est sans conteste issue de la biologie systématique et des théories de l'évolution (arbres phylogénétiques). C'est cependant à propos de filiation de manuscrits que Buneman (1971) importait, dans le monde du texte, des idées évolutionnistes, en comparant deux à deux les lexiques de manuscrits correspondant à des recopies successives d'une même source. En représentant, d’une manière approchée, les dissimilarités ainsi obtenues par les arêtes d'un arbre A on voit apparaître deux sortes de sommets : les sommets réels qui sont étiquetés par les manuscrits du corpus et des sommets latents qui correspondraient à des copies intermédiaires qui se seraient perdues. Plus de dix années plus tard un paradigme analogue était suivi par Abdi et al (1984). En particulier ces auteurs reprenant les très célèbres travaux de Bartlett (1932) sur la mémoire, utilisent des représentations arborées des lexiques de répétitions à divers instants d'un même texte (The war of the Ghosts, Bartlett, 1932, chap. 7) pour déterminer si les sujets ont tendance
- à reproduire, à l'instant t, la version produite à l'instant (t-1), ou bien
- à reproduire, à chaque instant, la version originale du récit.
Dans Luong (1988) et Barthélemy & Luong (1988) on trouve les premières utilisations d'arbres de types phylogénétiques pour représenter diverses entités lexicales liées à des données textuelles. Et en 1989 un ouvrage collectif était consacré à ce sujet (Luong, 1989). Pour prendre connaissance de divers autres contextes dans lesquels les représentations arborées de données ont été utilisées, le lecteur pourra se reporter à Barthélemy & Guénoche (1991).
D'une manière générale le problème de la représentation arborée d'une mesure de dissimilarité d sur un ensemble, supposé fini, X consiste à déterminer un arbre dont les feuilles, et éventuellement d'autres sommets, sont étiquetés par X (ce sont les sommets réels de Buneman, mentionnés plus haut) et dont les arêtes sont munies de longueurs > 0 de telle sorte que la somme des longueurs des arêtes qui constituent le chemin entre deux sommets réels x et y (appelée distance additive entre x et y) soit une "bonne approximation" de la dissimilarité d (x,y). Ce problème d'approximation, au sens des moindres carrés, ou de toute autre norme Lp, est NP-difficile (Day, 1987). La partie difficile du problème consiste à trouver une "bonne topologie d'arbre" sur laquelle projeter la dissimilarité d. Si celle-ci était connue on se trouverait ramené à un problème de programmation convexe assez banal (cf. Barthélemy & Guénoche, 1991). C'est dire que, en dehors de la tentative d'engendrer toutes les "topologies" et de conserver la meilleure après projection de la dissimilarité de départ (Ficht & Margoliash, 1967), fournissant une méthode ne pouvant s'appliquer qu'à de très petites tailles de données (7 ou 8), les algorithmes d'approximation que propose la littérature sont tous heuristiques. La plupart d'entre eux sont analysés dans Barthélemy & Guénoche (1991). Aux références que l'on peut trouver dans cet ouvrage il convient d'ajouter la méthode NJ (Saitou & Nei, 1987), devenue un standard en reconstruction phylogénétique (voir aussi Gascuel, 1994 ; Studier & Keppler, 1988 ; Nei, 1991), ainsi que quelques approches récentes (Berry & Gascuel, 1997 ; Gascuel & Lepy, 1996 ; Gonnet, 1994 ; Makarenkov, 1997).
Les heuristiques de représentation arborée peuvent être classées en trois catégories : approches métriques, géométriques et topologiques.
(i) Les approches métriques, visent à déterminer, plus ou moins directement, une distance arborée qui approche "au mieux" une mesure de dissimilarité donnée. Le problème, pris au sens des moindres carrés, est alors de résoudre la minimisation "assez tordue" ci-dessous
Min ·x,y (d(x,y)-¶(x,y))2, (0)
avec, pour tout x, y, z, t Œ X, ¶(x,y)+¶(z,t) _ Max(¶(x,z)+¶(y,t), ¶(x,t)+¶(y,z)).
(ii) Les approches géométriques font opérer des transformations sur l'ensemble X muni de la dissimilarité d. En effet, la condition, dite condition des quatre points,
¶(x,y)+¶(z,t) _ Max(¶(x,z)+¶(y,t), ¶(x,t)+¶(y,z)) (1)
qui caractérise les distances arborées peut être vue comme une propriété de l'espace métrique (X, ¶). On applique alors un opérateur O à la dissimilarité d de telle sorte qu'au bout d'un nombre fini q d'itérations, ¶ = Oq(d) vérifie la condition des quatre points (l'algorithme de Roux, 1988, suit ce paradigme).
(iii) Les approches topologiques privilégient la recherche d'une structure d'arbre qui reflète "au mieux" les données (Bandelt & Dress, 1986). C'est ainsi que n'importe quel algorithme de classification hiérarchique permet d'obtenir un arbre support sur lequel le problème (0) devient aisé à résoudre (Barthélemy & Luong, 1986, ce type d'approche est également discuté dans Barthélemy & Guénoche, 1991). La plupart des algorithmes "topologiques" sont cependant plus ou moins inspirés de ADTREE (Sattah & Tversky, 1977). Ils sont fondés sur l'observation que deux feuilles x et y d'un arbre (considérées comme des sommets réels) sont adjacentes à un même nœud si et seulement si pour toute paire z,t de sommets réels distincts de x,y on a, pour la distance additive ¶ de l'arbre :
¶(x,y)+¶(z,t) = Min(¶(x,z)+¶(y,t), ¶(x,t)+¶(y,z), ¶(x,y)+¶(z,t)) (2).
On définit alors le score de la paire x,y de sommets réels comme le nombre de sommets
réels z,t vérifiant l'égalité (2). ADTREE fusionne une paire de score maximal, réévalue la dissimilarité du nœud ainsi formé à tous les autres sommets réels (grâce aux égalités linéaires obtenues en plaçant ce nœud sur chaque chemin issu de x ou de y), le considère comme un sommet réel, recalcule les scores et ainsi de suite. A la fin de l'algorithme les longueurs d'arêtes de l'arbre ainsi créé sont réévaluées. Sous le nom de méthodes de groupement, Luong (1988) a proposé une variante à ADTREE beaucoup plus générale et un peu plus rapide qui s'en distingue sur essentiellement quatre points :
(i) Elles permettent de fusionner plus de deux éléments (on parle alors de groupement) de X (alors que ADTREE conduisait nécessairement à un arbre binaire).
(ii) Elles permettent d'obtenir des sommets réels qui ne sont pas des feuilles (on parle alors de groupement pointé).
(iii) Elles n'exigent pas de réévaluation des distances à chaque fusion : les paires sont rangées par ordre de score décroissant et fusionnées tant que un certain indice ne franchit pas un seuil critique.
(iv) Grâce, en particulier, à ces indices et seuil on peut évaluer la qualité des groupements produits par l'algorithme.
Mettre méthodes de groupement au pluriel est légitime car une instanciation donnée va dépendre du choix des indices et des seuils intervenant dans le point (ii). On l'a compris ce sont les préférées des auteurs. Cependant, même si elles ont reçu un certain nombre d'applications en analyse de données textuelles, - citons Luong, 1988 ; Barthélemy & Luong, 1988 ; Brunet 1988 ; Juillard, 1989 ; l’ouvrage collectif déjà cité (CUMFID 1989, Luong ed.) ; Maciel, 1993 ; Juillard 1994 ; Juillard & Luong, 1994 ; Mellet & Luong 1995 ; Maciel & Luong 1996 ; Juillard & Luong, 1997 ; Vilhena, 1997 - elles ne sont pas devenues des "classiques" (par exemple, dans le monde de la reconstruction phylogénétique, la méthode N.J., Saitou & Nei, 1987, reste "le" standard). Deux reproches leur sont généralement adressés :
(i) elles fournissent une approximation de la dissimilarité initiale moins bonne que celle que l'on obtiendrait à l'aide d'une approche métrique (ou géométrique).
(ii) Leur complexité algorithmique est trop élevée. La seule obtention de la liste des paires de sommets réels ordonnés par scores décroissant est en O(n4). Elle doivent donc être réservées à des corpus de taille moyenne (de l'ordre de tout ou partie de l'œuvre d'un auteur).
Le point (i) n'est pas étonnant. Les méthodes de groupement visent d'abord à déterminer une topologie pertinente et ensuite à projeter sur elle la dissimilarité. D'ailleurs des indices de type "topologique" (mais plus subtils d'interprétation qu'une corrélation ou un écart type) permettent de redresser la situation (Barthélemy & Guénoche, 1991 ; Gascuel, 1994 ; Guénoche, 1987)
Si l'on se restreint à des corpus de taille raisonnable, les inconvénients du point (ii) sont, selon nous, largement compensés par la richesse interprétative des méthodes de groupement. Tout en conservant, bien-sûr, la nature additive de la distance obtenue et donc la possibilité de l'interpréter en termes d'intermédiarité, voire de filiation, les algorithmes de groupements, procédant par fusions successives sont de nature classificatoire. Ils rendent compte d'une dialectique regroupement / opposition. C'est parce qu'elle s'oppose, via l'égalité (2) à (presque) toutes les autres paires d'objets qu'une paire x, y va fusionner. Les deux exigences, souvent contradictoires, de la classification automatique : homogénéité intra-classes et séparation inter-classes se trouvent ainsi réconciliées. Par ailleurs la variabilité des longueurs d'arêtes au sein d'un même groupement permet de rendre compte de phénomènes de typicalité (ou de représentativité, Barthélemy, 1991). Les groupements peuvent, en outre, être analysés au fur et à mesure qu'ils apparaissent. C'est à cette passionnante discussion que se livre Juillard (1989) sur les catégories grammaticales dans les poèmes de Day Lewis ; l’arbre n’est plus observé comme un produit fini mais c’est sa dynamique même, induite par l’algorithme de construction, qui est étudiée.
C'est à l'interprétation d'un arbre issu d'une méthode de groupements qu'est consacré le paragraphe qui suit (23 textes de Giraudoux comparés à l'aide de leur lexique). Ensuite on présentera l'algorithme utilisé de manière générique (utilisation itérative d'une relation dite de voisinage). Il synthétise et, espérons-nous, clarifie des présentations antérieures des méthodes de groupements. Sa lecture ne demande qu'une connaissance très minimale du vocabulaire de la théorie des graphes. Un lecteur peu intéressé par les aspects algorithmiques pourra cependant l'omettre et, muni des clés interprétatives fournies au paragraphe 1, passer directement au paragraphe 3 où sont arborisés
- les mots les plus fréquents chez Shakespeare,
- les catégories grammaticales observées sur une soixantaine de textes (Lob corpus),
- la ponctuation chez Émile Zola.
1. Pour introduire aux représentations arborées : comparaison des lexiques de 23 textes de Giraudoux.
L'indice de connexion lexicale (Muller, 1977 ; Brunet, 1988) permet de comparer les lexiques de deux textes. Il s'agit d'une adaptation du fameux indice de Jacquart (1908). La connexion lexicale fait intervenir les fréquences, ce qui est naturel pour des textes longs. Elle est fondée sur l'hypothèse que la répartition des occurrences des formes peut être construite à partir de comparaisons de tableaux de fréquences observés et des effectifs théoriques. Sa pertinence a été constatée par Barthélemy & Luong (1988). Il reste cependant trop peu utilisé, peut-être à cause de la complexité de son élaboration.
Nous allons, à titre d’exemple introductif, examiner la connexion lexicale entre 23 textes de Giraudoux, dans l'ordre chronologique de leur publication.
1 Pro Provinciales 2 Ind L’école des indifférents
3 Sim Simon le Pathétique 4 Suz Suzanne et le Pacifique
5 S&L Siegfried et le Limousin 6 Jul Juliette au pays des hommes
7 Bel Bella 8 Egl Eglantine
9 Sie Siegfried 10 Amp Amphitryon 38
11 Bar Aventures de Jérôme Bardini 12 Jud Judith
13 Int Intermezzo 14 Com Combat avec l’Ange
15 Gue La guerre de Troie n’aura pas lieu
16 Ele Electre 17 Can Cantique des cantiques
18 Elu Choix des Elues 19 Ond Ondine
20 Apo Apollon de Bellac 21 Sod Sodome et Gomorrhe
22 Fol La Folle de Chaillot 23 Luc Pour Lucrèce
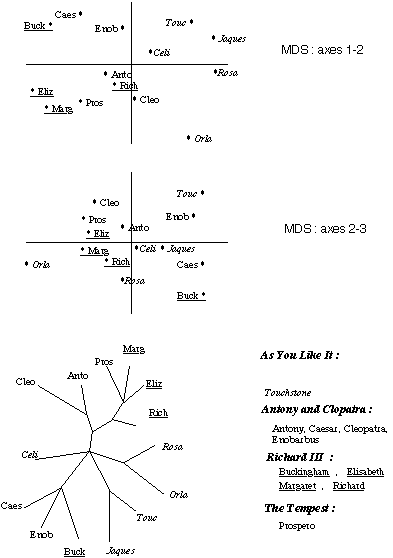
Le tableau 1 représente la matrice des connexions lexicales, Brunet (1978). Usuellement on interprète une telle matrice de proximité à l'aide d'analyses multivariées (multidimensionnal scaling, analyse factorielle des correspondances) ou de classifications. Les premières (figure 1-a) permettent de "visualiser" des proximités, les secondes d'ordonner par niveaux de finesse des classes 'homogènes" (figure 1-b). Notons que sur ces données la classification utilisée n’est pas très séparatrice.
Dans cet article nous allons examiner une autre approche : celle des représentations arborées. L'arbre de la figure 2 a comme feuilles nos 23 textes (rien n'empêcherait un sommet intérieur d'être également étiqueté), ses arêtes ont des longueurs variées. Il a été calculé de telle sorte que la longueur du chemin entre deux textes, somme des longueurs des arêtes qui le constituent, est une "bonne" approximation de leur connexion lexicale. Ici l'approximation
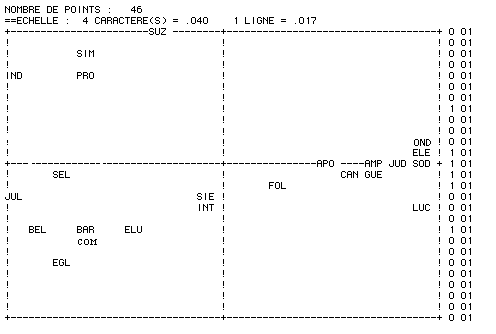
Figure 1-a : analyse factorielle des correspondances de la connexion
lexicale, axes 1-2

Figure 1-b : classification ascendante hiérarchique de la connexion
lexicale
n'est pas mauvaise puisqu'elle correspond à une corrélation de 0,93. Sa structure en éventail rend compte de la chronologie de l'écriture des œuvres.
PRO 0 14 19 24 25 25 26 29 31 35 27 33 28 24 34 35 22 25 36 23 37 29 37
IND 14 0 7 16 16 19 18 17 22 29 20 28 21 17 34 34 21 20 34 23 34 28 34
SIM 19 7 0 26 32 29 26 34 27 34 31 31 31 20 35 40 20 23 38 21 37 40 40
SUZ 24 16 26 0 38 34 40 46 34 38 38 36 36 23 41 46 20 25 39 19 37 41 46
SeL 25 16 32 38 0 22 21 35 26 42 37 37 29 20 38 48 22 24 44 21 43 36 46
JUL 25 19 29 34 21 0 19 25 33 40 24 40 30 18 44 55 24 23 47 26 45 41 50
BEL 26 18 26 40 21 19 0 22 27 42 25 36 29 18 42 48 23 21 46 24 41 34 42
EGL 29 17 33 46 35 25 22 0 30 39 23 38 32 16 40 49 22 21 45 24 40 42 43
SIE 31 22 27 34 26 33 27 30 0 28 30 26 21 23 28 31 16 22 29 19 32 29 31
AMP 35 29 34 38 42 40 42 39 28 0 35 18 25 28 19 23 17 27 24 18 19 37 25
BAR 27 20 31 38 37 24 25 23 30 35 0 35 32 18 40 47 23 19 46 22 39 42 43
JUD 33 28 31 36 37 40 36 38 26 19 35 0 28 25 21 19 14 27 23 15 19 30 16
INT 28 21 31 36 29 30 29 32 21 25 32 28 0 20 28 34 16 21 29 17 33 26 30
COM 24 17 20 23 20 18 18 16 23 28 18 25 20 0 26 30 18 12 33 20 32 25 28
GUE 34 34 35 41 38 44 42 40 28 19 40 21 28 26 0 21 16 29 22 18 22 32 25
ELE 35 34 40 46 48 55 48 49 31 23 47 19 34 30 21 0 14 28 21 20 20 33 19
CAN 22 21 20 20 22 24 23 22 16 17 23 14 16 19 16 14 0 16 14 13 15 15 13
ELU 25 20 23 26 24 23 21 21 22 27 19 27 21 12 29 28 16 0 29 21 27 25 24
OND 36 34 38 39 44 47 46 45 29 24 46 23 29 33 22 21 14 28 0 16 22 29 21
APO 23 23 22 19 21 26 24 24 19 18 22 15 17 20 18 20 13 21 16 0 15 16 14
SOD 37 34 37 37 43 45 41 40 32 19 39 19 33 32 22 20 15 27 22 15 0 37 16
FOL 29 28 40 41 36 41 34 42 30 37 42 30 26 25 32 33 15 25 29 16 37 0 28
LUC 38 34 40 46 46 50 42 43 31 25 43 16 30 28 25 19 13 24 21 14 16 28 0
Tableau 1 : la connexion lexicale de 23 oeuvres de Giraudoux
Les représentations arborées permettent de décliner divers types d'interprétations :
- Proximité, par exemple, L'Apollon de Bellac est proche du Cantique des cantiques tandis qu'Electre est fort éloigné, quant à l'utilisation du lexique, de Suzanne et le Pacifique et que la folle de Chaillot a une position excentrée.
- Classifications locales, c'est ainsi que sur l'arbre de la figure 2, les pièces anciennes apparaissent clairement : Amphitryon 38, Judith, La guerre de Troie n'aura pas lieu, Ondine, Electre, Sodome et Gomorrhe, Pour Lucrèce. A l'intérieur de cette classe, les deux dernières tragédies (chronologiquement), Sodome et Gomorrhe et Pour Lucrèce forment une paire qui se regroupe avec Electre.
- Globalement, une "dialectique" groupement / opposition : le gommage d'une arête éclate l'arbre en deux composantes connexes. Les textes d'une classe, se regroupant, s'opposent à ceux de l'autre (Buneman, 1971, à propos de filiation de manuscrits, appelait "scission" une telle bipartition). C'est ainsi que l'on voit sur la figure 2 le théâtre bien séparé du roman, et que, à l'intérieur du théâtre, les pièces antiques s'opposent aux pièces modernes ; tandis que du côté des romans on voit clairement apparaître trois périodes :
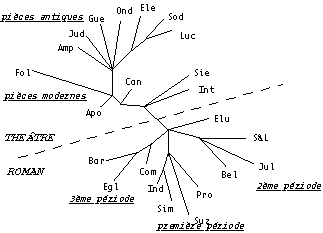
Figure 2
(i) les romans de début : Provinciales, L'École des Indifférents, proche de Simon le Pathétique et Suzanne et le Pacifique un peu plus excentré.
(ii) une seconde période assez homogène avec Siegfried et le Limousin, Juliette au pays des hommes et Bella.
(iii) Églantine et Aventures de Jérôme Bardini forment une paire que vient rejoindre le Combat avec l'Ange.
Le choix des Élues ne se rattache à aucun de ces trois groupes. Dernier roman de Giraudoux, il est proche, par la distance, du Combat avec l'Ange, roman qui le précède dans la chronologie
- Filiation et intermédiarité, c'est ainsi que le chemin qui va de la Folle de Chaillot jusqu'à Siegfried et le Limousin passe à proximité de l'Apollon de Bellac et du Cantique des Cantiques. Ces pièces courtes se trouvent près du centre de l'arbre. Par ailleurs Siegfried et Intermezzo, adaptations de romans pour le théâtre, sont réunis et dans une situation intermédiaire entre le groupe "théâtre" et le groupe "roman".
2. X-arbres et représentations arborées
2.1 Généralités
Nous supposons connues les définitions les plus élémentaires relatives aux arbres (le lecteur pourra se reporter à Barthélemy & Guénoche, 1991). Rappelons que, dans un arbre, une feuille est un sommet de degré 1 et un nœud est un sommet de degré > 1. Considérons un ensemble fini X, dont les éléments sont appelés étiquettes (pratiquement, dans cet article, les étiquettes sont des données textuelles) et rappelons qu'un X-arbre est la donnée d'un arbre A et d'une fonction, appelée étiquetage, f de X dans l'ensemble des sommets de A. On suppose que tous les sommets de degré _ 2 sont étiquetés.
Un sommet étiqueté est aussi appelé un sommet réel et un sommet non étiqueté est appelé un sommet latent. Lorsque chaque sommet latent ne reçoit qu'une étiquette (c. à d. lorsque la fonction f est injective) on dit que le X-arbre est séparé. Par exemple l'arbre de la figure 2 est séparé et tous ses sommets réels sont ses feuilles. Dans les dessins nous adoptons la convention qu'un sommet réel est noir et qu'un sommet latent est blanc.
Nous supposons désormais que tous les X-arbres qui interviennent dans cette étude sont séparés. On omettra la fonction f en désignant un sommet réel par son étiquette (on notera donc simplement un X-arbre par A).
Lorsque les arêtes de A sont munies de longueurs strictement positives, on définit la longueur d'un chemin comme la somme des longueurs des arêtes qui le constituent. La distance additive de A entre deux sommets réels est la longueur d(x,y) du chemin qui les relie.
2.2 Effeuillage d'un X-arbre
Soit un noeud s dans un arbre et k le nombre de feuilles qui lui sont directement attachées. On dit que s est un nœud périphérique s’il est de degré k+1.
Soit A un X-arbre, on dit que deux sommets réels x et y sont voisins, et on note xJy, si et seulement si x et y vérifient l'une des trois conditions ci-dessous :
(i) x et y sont deux feuilles adjacentes à un même nœud périphérique
(ii) x est une feuille et y un nœud périphérique adjacent à x
(iii) x = y
J est clairement une relation d’équivalence sur l'ensemble X des sommets réels de A. Ses classes d'équivalence sont appelées groupements. Ceux-ci se répartissent en deux types :
- les groupements homogènes : le nœud auquel les sommets réels de la classe sont adjacents n'est pas étiqueté ;
- les groupements pointés : le nœud auquel les feuilles de cette classe sont adjacents est étiqueté. Il appartient donc au groupement.
Dans tous les cas le nœud auquel les feuilles d'un groupement G sont rattachées est appelé nœud de G.
En gommant les arêtes incidentes aux feuilles d'un même groupement on obtient un nouvel arbre dont les feuilles, correspondant aux groupements, sont étiquetées par X/J . En réitérant cette opération sur notre nouvel ami le X/J-arbre, on construit un nouvel arbre et ainsi de suite (figure 3) …, on arrive finalement à un deux sommets réels liés par une arête ou à une étoile. Dans ce dernier cas, tous les sommets réels sont voisins et la dernière itération fournit un "arbre point " (figure 4).
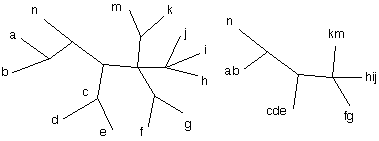
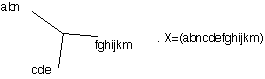
Figure 3

Figure 4 : configurations obtenues à la fin de l'algorithme d'effeuillage, sur un arbre
avec au plus trois sommets réels
2.3 Rhabillage d'un X-arbre
Cette opération est, en quelque sorte, l'inverse de l'effeuillage : si les itérées de la relation d'équivalence J sont connues, il est possible (et facile), en utilisant l'algorithme 1, de reconstituer le X-arbre A.
Algorithme 1
Tant que |X| _ 4 faire
{ Déterminer tous les groupements de A, les étiqueter à l'aide de l'ensemble X/J . Ces groupements sont les feuilles d'un X/J-arbre A'.
Faire X := X/J , A : = A' }
Fin de l’algorithme.
Supposons maintenant que A est valué. La distance additive de A permet de retrouver la relation J, donc -en vertu de ce qui précède- l'arbre A. Rappelons tout d'abord que d, en tant que distance sur X, est caractérisée par le fait que pour tout x, y, z, t Œ X, les deux plus grandes des trois sommes
d(x,y) + d(z,t), d(x,z) + d(y,t) et d(x,t) + d(y,z)
sont égales (condition dite des quatre points, cf. Barthélemy & Guénoche, 1991, pour une démonstation et une bibliographie). Cette condition caractérise une distance représentable par un X-arbre et celui-ci est le seul à représenter d. Ce résultat se comprend aisément si l'on considère la figure 5.
C'est en déclinant la condition des quatre points que nous allons retrouver la relation J.
Propriété 1. Soit A un X-arbre et x, y Œ X, on a xJy, si et seulement si pour tout z,t Œ X :
d(x,y) + d(z,t) _ d(x,t) + d(y,z) = d(x,z) + d(y,t).
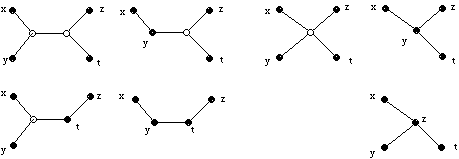
La figure 5 montre tous les cas possibles, lorsque les quatre sommets réels sont deux à deux distincts et à une transposition près des sommets x, y et/ou z, t. Les configurations de gauche (a) correspondent à :
d(x,y) + d(z,t) < d(x,t) + d(y,z) = d(x,z) + d(y,t),
celles de droite (b) à :
d(x,y) + d(z,t) = d(x,t) + d(y,z) = d(x,z) + d(y,t).
Le score fort, s*(x,y) d'une paire x,y de sommets réels est le nombre de paires z,t de sommets réels telles que :
d(x,y) + d(z,t) < d( x,t) + d( y,z) = d(x,z) + d(y,t).
Le score faible s(x,y) de x,y est le nombre de paires de sommets z,t telles que :
d(x,y) + d(z,t) _ d(x,t) + d(y,z) = d(x,z) + d(y,t).
 (a) (b)
(a) (b)
Figure 5
Ainsi a-t-on toujours s*(x,y) _ s(x,y). Par ailleurs, il est clair que :
Propriété 2. Soit x,y une paire de sommets réels issus d'un même groupement composé de k sommets réels, on a :
s*(x,y) = (n-k)(n-k-1)/2 et s(x,y) = (n-2)(n-3)/2
Désignons par k° la taille minimum d'un groupement de l'arbre A. Le score fort maximum des paires de sommets réels de A vaut alors
s** = (n-k°)(n-k°-1)/2 <= (n-2)(n-3)/2.
La propriété suivante mérite une démonstration. Le lecteur intéressé peut en prendre connaissance dans l'annexe technique.
Propriété 3. Deux sommets réels x et y sont voisins si et seulement si
s**- s(x,y) < (n-k°-1).
Comme on a toujours k° _ 2, on déduit de la propriété 3, la :
Propriété 4. Si deux sommets réels x et y ne sont pas voisins, alors :
s**- s(x,y)_ (n-3).
A partir de la structure de données décrite ci-dessous, on peut reconstituer la relation J et appliquer l'algorithme 1 pour reconstruire le X-arbre.
Structure de données : un tableau à deux colonnes, dans la première les paires de sommets réels sont rangées par ordre de score fort décroissant, dans la seconde est indiquée le score faible de chaque paire. On suppose aussi connue la valeur maximale du score fort.
La propriété 3 (ou 4, si l'on ne connaît pas k°) permet de bien distinguer les groupements les uns des autres. La reconstruction d'un X-arbre valué à partir de la relation J, ainsi inférée de sa distance additive peut paraître bien alambiquée. Sa pertinence va pourtant se manifester dans la détermination d'une "topologie arborée" (c. à d. d'un systèmes de groupements itérés) plausible relativement à une mesure de dissimilarité qui ne serait plus arborée. C'est alors la propriété 4 que nous utiliserons comme "test de voisinage".
La relation J étant obtenue à partir de la distance additive d de A, il est aisé de retrouver les longueurs des arêtes qui conduisent à A, soit localement, soit globalement.
- Localement, si x et y son reconnus voisins, donc éléments d'un même groupement G, on prend un troisième sommet réel z et on résout le système d'équations linéaires à trois inconnues relativement à : la longueur de l'arête entre x et le nœud u de G, la longueur de l'arête entre y et u, la longueur du chemin entre u et z.
- Lorsque l'arbre est reconstruit, on écrit comme précédemment le système d'équations linéaires qui décompose les distances d(x,y) en sommes des longueurs des arêtes du chemin joignant x et y.
2.4 Représentations arborées
Les notions introduites ci-dessus s'adaptent mutatis mutandis au cas où X est décrit par une mesure de dissimilarité quelconque d (non nécessairement arborée). Les éléments de X sont alors appelés des objets.
La notation suivante nous simplifiera la vie : si un seul élément de la famille (ui) de nombres réels est minimum, on le désigne par Min* (ui).
Le d-score fort d'une paire x, y d'objets est le nombre s*(x,y) de paires d'objets z, t , distincts de x, y, tels que :
d(x,y)+d(z,t) = Min*(d(x,z)+d(y,t), d(x,t)+d(y,z), d(x,y)+d(z,t)).
Le d-score faible de x, y de X est le nombre s(x,y) de paires d'objets z, t, distincts de x, y tels que :
d(x,y)+d(z,t) = Min(d(x,z)+d(y,t), d(x,t)+d(y,z), d(x,y)+d(z,t)).
On définit séquentiellement la liste des objets d-prévoisins de la manière suivante :
- si s*(x,y) est la valeur maximum s** des scores stricts des paires d'objets, alors x et y sont d-prévoisins,
- si pour tous z,t tels que s*(z,t) > s*(x,y) z et t sont d-prévoisins et si s**-s(x,y) > (n-3), alors x et y sont d-prévoisins.
"x et y sont d-prévoisins" définit une relation binaire J°(d) qui, en général n'est pas transitive ; on note par J (d) et on appelle équivalence de voisinage la fermeture transitive de J°(d). J(d) est une relation d'équivalence.
Une classe d'équivalence modulo J(d) est appelée un d-groupement.
Lorqu'un groupement est formé de deux objets x et y seulement, on peut évaluer la dissimilarité entre {x,y} et les objets z non classés dans G :
d({x,y}, z) = 1/2 (d(x,z)+d(y,z)-d(x,y)).
Notons que cette quantité ne sera non négative que si l'inégalité triangulaire est vérifiée pour x, y et z.
Dans le cas général on pose
d(G,z) = 2/k(k-1) ·x,yŒGd({x,y}, z).
On en déduit alors une évaluation d(G,G') de la dissimilarité entre deux groupements G et G', on en déduit une extension d/J de d à X/J :
d/J(G,G') = Max(0, d(G, G').
On peut alors énoncer :
Algorithme 2
Tant que |X| > 3 faire
{Calculer la relation J, déterminer l'ensemble quotient X/J et la dissimilarité d/J.
Faire X := X/J, d := d/J. }
Fin de l’algorithme.
En considérant qu'à chaque itération les groupements vont s'accrocher aux feuilles d'un X-arbre celui-ci est construit de proche en proche. A la fin de l'algorithme il suffit de réévaluer, au sens des moindres carrés, sa distance additive.
On notera que sous la forme générique que nous avons choisie, l'algorithme 2 rend compte (modulo les choix de J et de d/J) de pratiquement n'importe quel algorithme de classification ascendante hiérarchique.
3. Trois applications : les mots les plus fréquents dans quatre pièces de Shakespeare, le LOB corpus et les catégories grammaticales, la ponctuation chez Zola.
3.1 Les données de Horton concernant quatre pièces de Shakespeare
Nous traitons les données de Horton [1991] concernant des personnages de quatre pièces de théâtre de Shakespeare.

Figure 6 : Shakespeare, les mots les plus fréquents.
Les représentations planes de la figure 6 ont été obtenues, avec la distance euclidienne construite à partir d'une liste de 40 mots les plus fréquents, par le Multidimensional Scaling (MDS) (cf Kruskal [1963], Shepard [1980]), dans un espace à quatre dimensions. L'aspect le plus frappant est la grande valeur sur l'axe 2 des personnages de As You Like It, en nette opposition avec Buckingham, Elizabeth et Margaret, trois des quatre personnages de Richard III. Ces personnages semblent se situer bien loin du rôle principal Richard, mais cela est contredit par le plan 2-3 où Richard se rapproche nettement des deux héroïnes et où Buckingham s'en éloigne. C'est aussi dans le plan 2-3 que l'on voit confirmer le rapprochement de Antony et Cleopatra. En calculant le stress sur ces données, MDS indique que l'espace significatif est de dimension quatre, ce qui rend encore plus difficile la lecture des résultats.
L'arbre de la figure 6 montre de manière plus nette ces oppositions et regroupements. Les deux héroïnes Celia et Rosalind de As You Like It sont sur deux branches opposées de l'arbre : les fréquences des mots utilisés par chacune diffèrent très sensiblement. Sur l'arbre, les personnages de cette pièce ne côtoient pas les héros des trois autres. La chronologie joue-t-elle un rôle déterminant dans cette distribution du vocabulaire, ou bien est-ce une caractéristique de la pièce ?
3.2 Le Lob Corpus (distance du khi-2)
Le Lob Corpus se compose de 500 échantillons d'environ 2500 occurrences représentant la plupart des domaines de la langue écrite et tous provenant d'œuvres et de documents divers publiés en langue anglaise au cours de l'année 1961 et regroupés en grandes catégories : presse, sciences, religion, fiction...(Johansson [1980]). La version codée, apparue dans le cours des années 80, enrichit d'informations considérables la base textuelle de départ. Un premier travail, Juillard & Luong [1994], effectué sur ce corpus consistait à rechercher des structurations grammaticales dans divers genres littéraires. Nous en extrayons ici deux exemples dans le but de comparer deux points de vue différents : la classification hiérarchique et la représentation arborée.
3.2.1 Catégories grammaticales
La figure 7 montre une classification hiérarchique et une représentation arborée des onze catégories grammaticales sur un ensemble de soixante textes. On a utilisé la distance du c2 construite à partir du tableau des occurrences des catégories grammaticales dans les textes.
L'interjection a une faible distribution. Dans le dendrogramme de la classification elle se regroupe en dernier avec les autres classes, dans l'arbre elle rejoint à bonne distance le groupe prédicatif. La classification oppose deux classes ; en premier, le noyau verbal est composé des verbes, des adverbes et des auxiliaires et modaux auxquels se joignent les conjonctions de subordination ; en second, le groupe nominal dont le cœur est la classe composée des noms et des déterminants, se regroupant de manière assez proche avec les prépositions, les adjectifs, et puis plus loin avec les conjonctions de coordination. Les pronoms sont assez éloignés de ces deux classes.
Dans l'arbre, les pronoms rejoignent plutôt le groupe verbal composé du groupement verbes-adverbes, lequel avec les auxiliaires modaux forme un autre groupement. Le groupe nominal est constitué d'un groupement solide composé des noms, déterminants, prépositions et adjectifs. Les phénomènes les plus intéressants concernent la position intermédiaire des conjonctions de coordination et la relative indépendance des conjonctions de subordination. Il faudrait étudier de plus près ces textes pour émettre des conjectures. Nous renvoyons le lecteur à Juillard & Luong (1994) où l'on trouvera aussi les données traitées ici.
 r = 0.83 r = 0.97
r = 0.83 r = 0.97
Figure 7 : classification hiérarchique et représentation arborée de onze catégories
grammaticales
3.2.2 Les coordonnants
La figure 8 montre la classification hiérarchique et la représentation arborée de huit coordonnants. De la classification ne ressorte que deux couples de conjonctions de coordination : and-nor, yet-but - les autres conjonctions (4 sur 8) sont intégrés avec peine (either, neither) ou laissées à l’écart de la hiérarchie (then,or).
La représentation arborée est plus fine. Les deux couples unis précédemment dégagés (and-nor et but-yet) subsistent et occupent la partie centrale de l’arbre. Les deux conjonctions corrélatives either et or forment un ensemble conforme à leur rôle dans les énoncés. La conjonction neither est le pendant de either dans la partie droite de l’arbre. Le groupe lâche que cette conjonction forme avec then complète la silhouette équilibrée de la figure arborescente et ce rapprochement exprime des analogies de fréquence autant que de contenu et de comportement dans les textes.

Figure 8 : classification hiérarchique et représentation arborée de huit coordonnants
dans le Lob-corpus.
3.3 La ponctuation chez Émile Zola
3.3.1 Les données
Les données sont les occurrences des signes de ponctuation dans 22 romans de Zola, (Brunet,1985, page 104). Les romans sont numérotés de 1 à 22, suivant l’ordre chronologique :
1 Thérèse Raquin, 2 Madeleine Ferrat, 3 La fortune des Rougon
4 La curée, 5 Le ventre de Paris, 6 La conquête de Plassans
7 La faute de l’abbé Mouret, 8 Son excellence Eugène Rougon
9 L’assommoir, 10 Une page d’amour, 11 Nana
12 Pot Bouille, 13 Au bonheur des dames, 14 La joie de vivre
15 Germinal, 16 L’Oeuvre, 17 La terre
18 Le rêve, 19 La bête humaine, 20 L’argent
21 La débâcle, 22 Le docteur Pascal
3.3.2 L’arbre des romans
L’arbre des romans selon les signes de ponctuations est représenté par la figure 9. En associant chaque oeuvre son rang chronologique, on constate une corrélation presque parfaite entre le déroulement du temps et la publication des œuvres.
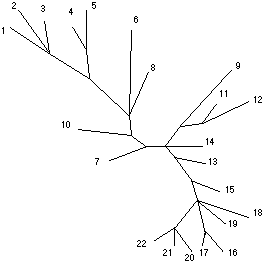
Figure 9
3.3.3 Les arbres des ponctuations
La figure 10 représente deux arbres. Le premier, à gauche, est l’arbre des ponctuations des 12 premières œuvres et le second est celui des 10 dernières œuvres. La comparaison de ces arbres est fort instructive. Le premier présente une structure incontestablement arborée. Le haut du schéma réunit les ponctuations terminales d’une part d’énoncés non déclaratifs, donc transformés (! et ?), d’autre part d’énoncés appelant complément ou remise en cause
(... et tiret).
C’est au contraire une structure en étoile que nous livre l’arbre des œuvres tardives. Le point et le point-virgule sont maintenant dissociés l’un de l’autre et se sont rapprochés de deux ponctuations de moindre importance (tiret et :) qui se trouvaient réunies dans la précédente configuration. La spécificité de chaque signe se trouve ainsi soulignée et l’équilibre de l’ensemble est comme l’image de la maturité stylistique de Zola dans l’agencement et le rythme de sa phrase.
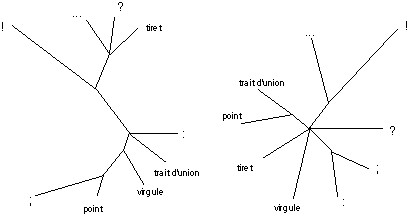
Figure 10
Annexe technique : démonstration de la propriété 3.
Propriété 3. Deux sommets réels x et y sont voisins si et seulement si
s**-s(x,y) < (n-k°-1).
Évaluons dans un premier temps la quantité Æ = s**-s(x,y) lorsque x et y ne sont pas voisins. Clairement, le minimum de Æ est atteint lorsque x appartient à un groupement G° de taille minimum et lorsque l’on est dans un des deux cas suivants :
- y est un nœud z adjacent au nœud de G°
- y est une feuille n’admettant aucun voisin et adjacente à z.
Dans les deux cas, on a :
Æ = 1/2 [(n-k°)(n-k°-1) - (n-k°-1)(n-k°-2)] = (n-k°-1). On en conclut que lorsque x et y ne sont pas voisins Æ _ (n-k°-1), ou encore que :
si s(x,y) > (n-k°) (n-k°-1)/2 + (n-k°-1) alors x et y sont voisins.
Réciproquement, supposons que x et y sont voisins, on a alors (par la Propriété 2) s(x,y) = (n-2)(n-3)/2. Remarquons aussi que, nécessairement on a 2 _ k° _ n/2. Le résultat sera donc acquis si l'on sait constater que pour tout entier k tel que 2 _ k _ n/2, on a :
(n-1)(n-2) > (n-k)(n-k-1) + 2(n-k-1).
Or la différence (n-1)(n-2) - (n-k)(n-k-1) - 2(n-k-1) vaut :
2kn-k2-4n+k+4 < 2kn-k2-4n+k. Cette dernière quantité s'annule pour k = n et pour k = 1/2, elle est donc strictement positive pour 2 _ k _ n/2.
Références
Abdi, H., Barthélemy, J.-P.& Luong, X. (1984). "Tree representation of associative structures in semantic and episodic memory research", in Trends in Mathematical Psychology (E. Degreef & J. Van Buggenhaut, eds.), Amsterdam : Elsevier Science Publishing (North-Holland), 3-31.
Bandelt, H.J. & Dress, A. (1986). "Reconstructing the shape of a tree from observed dissimilarity data ", Advances in Applied Mathematics 7, 309-343.
Bartlett, F.C. (1932). Remembering : a study in Experimental ans Social Psychology, Cambridge : Cambridge University Press.
Barthélemy, J.-P. (1991). "Similitude, arbres et typicalité", in Sémantique et Cognition (D. Dubois, ed.), Paris : Edition du CNRS, Collection Sciences du Langage 31, 205-224.
Barthélemy, J.-P. & Guénoche A. (1991). Trees and proximity representations, New York : John Wiley & Sons (première édition française : Les arbres et les représentations des proximités, Paris : Masson 1988).
Barthélemy, J.P. & Luong, N.X. (1986). "Représentations arborées des mesures de dissimilarités", Statistique et Analyse des Données, Paris.
Barthélemy, J.P. & Luong, N.X. (1988). "Sur la topologie d'un arbre phylogénétique : aspects théoriques, algorithmiques et applications à l'analyse des données textuelles", Math. et Sciences Humaines, Paris.
Berry, V. & Gascue, l O. (1997). "Nouveaux résultats autour des méthodes de reconstruction phylogénétiques basées sur les quadruplets", Actes des cinquièmes rencontres de la Société Francophone de Classification, Lyon, 319-322.
Brunet, E. (1978). Le vocabulaire de Jean Giraudoux structure et évolution, Slatkine : Genève.
Brunet, E. (1985). Le vocabulaire de Zola. Genève-Paris : Slatkine-Champion.
Brunet, E. (1988). "Une mesure de la distance intertextuelle : la connexion lexicale", in Le nombre et le texte, Revue Informatique et Statistique dans les Sciences humaines, Université de Liège.
Buneman, P. (1971). "The recovery of trees from measures of dissimilarity", in Mathematics in Archeological and Historical Sciences. Hodson & al. Eds, Edinburgh University Press.
Day, W.H.E. (1987). "Computational complexity of inferring phylogenies from dissimilarity measures", Bulletin of Mathematical Biology 49, 461-467.
Ficht, W.M. & Margoliash, E. (1967). "A non sequential method for constructing trees and hierarchical classifications", Journal of molecular evolution 18, 30-37.
Gascuel, O. (1994). "A note on Sattah and Tversky's, Saitou and Nei’s and Studier and Keppler's algorithms for inferring phylogenies from evolutionary distances", Molecular Biology and Evolution 11 (6), 961-963.
Gascuel, O. & Lepy, D. (1996). "A reduction algorithm for approximating a (nonmetric) dissimilarity by a tree distance", Journal of Classification 13, 129-155.
Gonnet, G. H. (1994). "New algorithms for the computation of evolutionary phylogenetic trees", in Computational Methods in Genome Research, (S. Sulai, ed.), New York : Plenum Press.
Guénoche, A. (1987). "Cinq algorithmes d'approximation d'une dissimilarité par des arbres à distances additives", Mathématiques et Sciences Humaines 98, 21-40.
Horton, T. B. (1991). "Frequent Words, Authorship, and Characterization in Jacobean Drama", in Research in Humanities Computing (Hockey S. & Ide N. eds.), 47-69, Oxford University Press.
Jaccart, P., (1908). "Nouvelles recherches sur la distribution florale", Bull. Soc. Vand. Sci. Nat., 44.
Juillard, M. (1989). "La dynamique de l'arbre : linguistique et représentation arborée", in Analyse arborée des données textuelles, Luong X. (ed.), CUMFID 16, Nice : CNRS.
Juillard, M. (1994). "Entre le silence et les bruits : les arbres" Travaux du cercle linguistique de Nice 16.
Juillard, M. & Luong, X. (1994). "De nouveaux arbres pour un nouveau corpus", in Revue Informatique et Statistique dans les Sciences humaines, CIPL-LASLA, 30, 37-51, Liège.
Juillard, M. & Luong, X. (1997). "Words in the Hood : A New Look at the distribution of Words in Texts", Literary and Linguistic Computing, vol 12, N°2.
Johansson, S. (1980). "The LOB corpus of British Texts : Presentation and Comments", ALLC Journal, 1,.25-36.
Kruskal, J. B.(1983). "Multidimensional Scaling by optimizing goodness of fit to a nonmetric hypothesis", Psychometrika, vol 29, 115-129.
Luong, N. X. (1988). Méthodes d'analyse arborée. Algorithmes. Applications. Thèse de doctorat d'état. Université de Paris V.
Luong, N.X. (ed.) (1989). Analyse arborée des données textuelles. Tree Analysis of Textual Data, CUMFID 16, Nice : CNRS - INLF.
Luong, N. X. & Maciel, C. (1993). "Les textes constitutionnels portugais (de 1971 à 1989). Environnement lexical - références et préférences du texte juridico-politique.", in JADT 1993 Secondes journées internationales d'analyse statistique de données textuelles Montpellier.
Luong, N. X. & Maciel, C. (1996). "Le texte juridico-politique. Un discours de pouvoir. Analyses arborées". in Projet Portext ; CUMFID 17, Nice : CNRS.
Luong, X. & Mellet, S. (1995). "Les calculs multidimensionnels au service de l’analyse syntaxique diachronique", in III Giornale internazionali di Analisi Statistica dei Dati Testuali JADT 1995, Roma.
Makarenkov, V. (1997). Propriétés combinatoires des distances d'arbre. Algorithmes et applications, Thèse (École des Hautes Études en Sciences Sociales, Paris et Institut des Sciences du Contrôle, Moscou).
Muller, Ch. (1977). Principes et méthodes de statistique lexicale, Paris : Hachette.
Nei, M. (1991). "Relative efficiencies of different tree-making methods for molecular data", in Phylogenetic analysis of DNA sequences (M. Miyamoto & J. Cracroft, eds.), Oxford : Oxford University Press, 90-128.
Roux, M. (1988). "Techniques of approximation for building for building two tree structures", in Recent Developments in Clustering and Data Analysis (C. Hayashi, E. Diday, M. Jambu & N. Oshum, eds), New York : Academic Press, 151-170.
Saitou, N. & Nei, M. (1987). "The neighbor-joining method : a new method for reconstructing phylogenetic trees", Molecular Biology Evolution 4, 406-425.
Sattath, S. & Tversky, A. (1977). "Additive similarity tree", Psychometrika, vol 42, 3, p319-345.
Shepard, R. N. (1980). "Multidimensional Scaling, tree-fitting and clustering", Science, 210, 390-398.
Studier, J.A. & Keppler, K.J. (1988). "A note on the neighbor-joining method of Saitou and Nei", Molecular Biology and Evolution 6 (5), 729-731.
Vilhena, A. M. (1997). L’évolution du vocabulaire de l’oeuvre littéraire de Manuel Alegre de 1960 à 1993, Paris : Slatkine-Champion.