Analyse de tableaux ternaires de données textuelles
Zárraga, A.
etpzacaa@bs.ehu.es
Departamento de Economía Aplicada III,
Universidad del País Vasco-Euskal Herriko Unibertsitatea
Bilbao, España
Goitisolo, B.
etpgoleb@bs.ehu.es
Departamento de Economía Aplicada III,
Universidad del País Vasco-Euskal Herriko Unibertsitatea
Bilbao, España
Abstract. Factorial analysis of a 3-way frequency table is generally performed by
correspondence analysis or, less frequently, by intra analysis. This requires
that data be reduced to a 2-way table by means of the sum or juxtaposition of
the binary tables of which it is composed. However those tables have a series
of peculiarities which are not considered in this procedure, resulting in a
joint analysis in which the internal relationships of each table may be
altered. This paper is a brief presentation of the Simultaneous Analysis which
enables the internal relationships of each table to be maintained. An
application of this method to the study of a 3-way lexical table is also
presented.
Keywords :
Factorial Analysis, Textual
Data, Simultaneous Analysis
Résumé. L' analyse
factorielle d' un tableau de fréquences ternaire s' effectue
habituellement par une Analyse de Correspondances ou, moins fréquemment, à
travers une Analyse Intra. Cela exige de réduire les données à un tableau
binaire par la somme ou juxtaposition des tableaux binaires qui le composent.
Toutefois, ces tableaux présentent une série de particularités qui ne sont
guère prises en considération dans cette manière de procéder, provoquant une
analyse conjointe dans laquelle les relations internes de chaque tableau
peuvent se trouver altérées. Dans ce travail, on présente brièvement
l' Analyse Simultanée qui permet de maintenir les relations internes de chaque
tableau et l' on offre une application de celui-ci à l' étude
d' un tableau lexical ternaire.
Mots-clés : Analyse Factorielle, Tableau lexical, Analyse Simultanée
1. Introduction
L' analyse statistique de données textuelles comme, par
exemple, celles provenant d' une enquête qui contient une ou plus
d' une questions ouvertes commence fréquemment par la mise en place
d' un tableau de contingence qui croise, d' une part, les mots
utilisés dans les réponses à la ou aux questions ouvertes et, d' autre
part, les caractéristiques des répondants (sexe, classes d' âge, niveaux
d' études, etc.). L' analyse de ce tableau à travers l' Analyse
Factorielle des Correspondances (AFC) offre principalement:
-
une structure sur les catégories des caractéristiques
des personnes interrogées. De sorte que soient mises en évidence quelles sont
les catégories considérées semblables dans la mesure où elles utilisent les
mêmes mots.
-
une structure sur les mots utilisés par les répondants.
De sorte que soient mis en évidence quels sont les mots employés par les mêmes
catégories d' individus.
Il peut être souhaitable, néanmoins, de recourir
à l' analyse globale d' une succession de tableaux de contingence du
type "mots x catégories d' une caractéristique (par ex. classes
d' âge) x catégories d' autre caractéristique (par ex. sexe)"
provenant d' un tableau ternaire, défini par le croisement de trois
variables. La méthodologie utilisée de manière classique [LEB 88], [LEB 94],
[LEB 98] et [BEC 00 a] consiste dans les AFC séparées des différents tableaux
de contingence et/ou dans l' Analyse Factorielle des Correspondances de la
juxtaposition des tableaux (dans le cas où les lignes des tableaux seraient
communes). Toutefois, les résultats découlant de cette manière de procéder
peuvent en être affectés, comme on le signale dans [BEC 00 b] par:
- Les
différences entre les profils des marges-en-ligne des différents tableaux.
- L' importance
relative des tableaux dans l' analyse, mesurable au travers des
contributions des colonnes, elle-même due:
·
à des différences entre les nombres totaux des
tableaux: "toutes choses égales par ailleurs", un tableau influence
d' autant plus l' analyse que son effectif total est important.
·
à des différences d' intensité de structure entre
les tableaux: "toutes choses égales par ailleurs", un tableau
influence d' autant plus l' analyse globale que sa structure est
forte.
Ces auteurs ont récemment proposé
l’Analyse factorielle multiple de tableaux de contingence pour tenter de donner
une solution aux problèmes mentionnés. Néanmoins, comme eux-mêmes le font
remarquer, cette méthodologie n’est appropriée que si les marges-en-ligne des
tableaux sont égales ou très proches entre elles.
L' Analyse Simultanée [ZAR
02] permet que les marges-en-lignes des tableaux soient différentes et permet de donner une solution aux
inconvénients indiqués en fournissant une description conjointe des différentes
structures contenues à l' intérieur de chacun des tableaux ainsi
qu' une comparaison de ces structures. Dans [ZAR 02] on vérifie, par
l' application à des données réelles, les différences entre la méthode
exposée et les méthodes existantes, notamment l' Analyse de
Correspondances du tableau somme, l' Analyse de Correspondances de la
juxtaposition et par rapport à l' analyse intra [ESC 88]. On vérifie
comment l' étude conjointe des relations internes à l' intérieur de
chaque tableau est possible et l' utilité de l' Analyse Simultanée,
en particulier, quand il existe des différences dans les totaux, dans les
marges-en-ligne ou dans l' intensité de structure entre les tableaux.
Dans le présent travail, cependant, on ne présente pas des
comparaisons avec les méthodes mentionnées d’analyse des données
textuelles, étant donné que celles-ci
sont déjà connues et que la base de données utilisée dans l’application se
trouve dans la base de données du logiciel SPAD (version 5.0) sous le nom de
Enq_nt.sba (§ 3), à portée de quiconque désire faire les analyses
opportunes.
L' objectif du présent travail
n' est donc pas tant d' approfondir dans la statistique textuelle que
de présenter l' Analyse Simultanée en tant que méthode venant compléter la
méthodologie existante d' analyse de données textuelles.
2. Méthodologie:
l' Analyse Simultanée de plusieurs tableaux de contingence
Soit 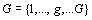 l' ensemble des
tableaux de contingence à analyser (figure 1).
l' ensemble des
tableaux de contingence à analyser (figure 1).
|
|
Tableau
1
|
|
|
|
Tableau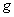
|
|
|
|
Tableau
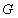
|
|
|
|
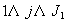
|
|
|
|
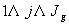
|
|
|
|
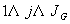
|
|
|
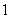
|
|
|
|
1
|
|
|
|
1
|
|
|
|
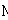
|
|
|
|
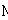
|
|
|
|
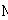
|
|
|
|
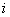
|
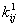
|
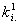
|
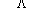
|
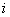
|
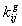
|
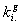
|
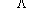
|
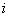
|
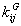
|
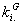
|
|
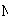
|
|
|
|
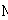
|
|
|
|
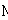
|
|
|
|
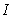
|
|
|
|
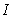
|
|
|
|
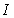
|
|
|
|
|
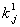
|
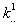
|
|
|
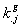
|
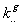
|
|
|
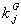
|
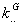
|
Figure 1: Succession de tableaux
Chacun d' entre eux classifie les réponses de 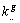 individus à deux
variables qualitatives codifiées en modalités. Tous les tableaux ont une des
variables (dont les modalités,
individus à deux
variables qualitatives codifiées en modalités. Tous les tableaux ont une des
variables (dont les modalités, 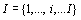 , se retrouvent dans les lignes) en commun. L' autre
variable de chaque tableau de contingence peut être la même ou différente,
codifiée de la même manière ou d' une manière différente. Les modalités de
la seconde variable de chaque tableau
, se retrouvent dans les lignes) en commun. L' autre
variable de chaque tableau de contingence peut être la même ou différente,
codifiée de la même manière ou d' une manière différente. Les modalités de
la seconde variable de chaque tableau 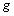 sont
sont 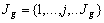 . En juxtaposant tous ces tableaux de contingence, on obtient
un ensemble
. En juxtaposant tous ces tableaux de contingence, on obtient
un ensemble 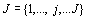 de colonnes.
de colonnes.
Si la succession de tableaux de
contingence provient d' un tableau ternaire, les modalités 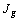 ,
,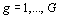 sont communes aux
sont communes aux 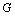 tableaux.
L' Analyse Simultanée est, cependant, extensible à l' étude de
tableaux avec différentes modalités en colonnes.
tableaux.
L' Analyse Simultanée est, cependant, extensible à l' étude de
tableaux avec différentes modalités en colonnes.
Pour solutionner
les problèmes indiqués au § 1, la méthode d' analyse de la
juxtaposition des tableaux doit permettre:
-
d' équilibrer l' influence des tableaux en
ajustant l' effectif de chacun des tableaux.
-
d' équilibrer l' influence des tableaux selon
les différences d' intensité de structure entre les tableaux.
-
de conserver dans une analyse factorielle globale aussi
bien les poids que la métrique de chacun des tableaux.
L' élément
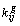 , correspond au nombre total d' individus qui
choisissent simultanément les modalités
, correspond au nombre total d' individus qui
choisissent simultanément les modalités 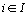 de la première variable et
de la première variable et 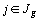 de la seconde variable (appartenant au tableau
de la seconde variable (appartenant au tableau 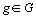 ).
).
L' Analyse Simultanée ajuste
les effectifs des tableaux comme le premier pas pour équilibrer
l' influence des tableaux. Pour cela, chacun des tableaux de contingence
est transformé, en le divisant par 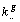 , total du g-ième tableau,
, total du g-ième tableau, 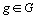 , en un tableau de fréquences relatives.
, en un tableau de fréquences relatives.
On notera:
Afin de contrôler l' influence dans l' analyse
globale des tableaux avec la plus forte structure, l' Analyse Simultanée
introduit une pondération, que nous appelons 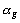 ,
, 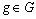 , sur chacun des groupes (ici les tableaux de contingence).
Cette pondération dépendra des inerties qui résultent d' une analyse des
correspondances simples de chacun des tableaux traités séparément. Ces inerties
pour le tableau
, sur chacun des groupes (ici les tableaux de contingence).
Cette pondération dépendra des inerties qui résultent d' une analyse des
correspondances simples de chacun des tableaux traités séparément. Ces inerties
pour le tableau 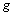 ,
, 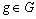 , seront notées
, seront notées 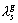 (l' inertie
projetée sur l' axe
(l' inertie
projetée sur l' axe 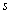 ,
, 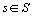 ) et
) et 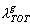 (l' inertie
totale). La pondération peut être équivalente à celle de l' analyse
factorielle multiple [ESC 84] pour variables continues
(l' inertie
totale). La pondération peut être équivalente à celle de l' analyse
factorielle multiple [ESC 84] pour variables continues 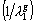 , celle équivalente à la méthode Statis [LHE 76],
, celle équivalente à la méthode Statis [LHE 76], 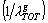 pour privilégier des
groupes de dispersion minimale, 1 si on ne veut pas de pondération sur les
tableaux, etc.
pour privilégier des
groupes de dispersion minimale, 1 si on ne veut pas de pondération sur les
tableaux, etc.
Si l' on
considère 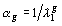 ,
, 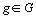 , pondération adoptée dans l' exemple
d' application (§ 3), la première valeur propre de l' analyse
factorielle de l' ensemble des tableaux de contingence sera comprise entre
0 et G. Si on veut rester dans le cadre de l' analyse des correspondances
et que la première valeur propre de l' analyse de l' ensemble des
tableaux soit comprise entre 0 et 1, il suffira d' adopter
, pondération adoptée dans l' exemple
d' application (§ 3), la première valeur propre de l' analyse
factorielle de l' ensemble des tableaux de contingence sera comprise entre
0 et G. Si on veut rester dans le cadre de l' analyse des correspondances
et que la première valeur propre de l' analyse de l' ensemble des
tableaux soit comprise entre 0 et 1, il suffira d' adopter 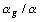 comme pondération avec
comme pondération avec 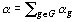 .
.
Enfin, pour que chaque tableau conserve ses poids et sa
métrique dans l' analyse globale, la méthode que nous présentons exige des
transformations dans les nuages de profils-colonnes et de profils-lignes que
l' on détaille ci-après.
2.1 Analyse
des colonnes
À chacun des 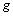 ,
, 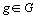 , tableaux de contingence est associé un sous-nuage,
, tableaux de contingence est associé un sous-nuage, 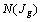 , de
, de 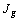 profils-colonnes
centrés:
profils-colonnes
centrés:
avec les poids 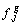 ,
, 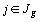 , et la métrique de matrice associée la matrice diagonale des
, et la métrique de matrice associée la matrice diagonale des
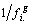 ,
, 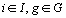 .
.
Pour analyser les tableaux
ensemble, nous sur-pondérons chaque sous-nuage par 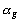 ,
, 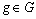 et comme ils sont tous situés dans le même espace,
et comme ils sont tous situés dans le même espace, 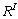 , nous considérons le nuage global,
, nous considérons le nuage global, 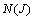 , qui englobe les
, qui englobe les 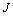 profils-colonnes.
Dans ce nuage, les métriques sont différentes pour chaque sous-nuage de profils
du même tableau, ce qui peut sembler empêcher l' analyse conjointe.
profils-colonnes.
Dans ce nuage, les métriques sont différentes pour chaque sous-nuage de profils
du même tableau, ce qui peut sembler empêcher l' analyse conjointe.
On peut
transformer les profils-colonnes de chacun des tableaux pour considérer leurs
distances euclidiennes. Dans l' analyse conjointe cela signifie considérer
les profils-colonnes:
avec les
poids 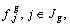 et la métrique
euclidienne usuelle.
et la métrique
euclidienne usuelle.
Dans cette analyse, les distances
euclidiennes entre profils-colonnes du même sous-nuage respectent les distances
du 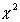 dans le sous-nuage original.
dans le sous-nuage original.
2.2 Analyse
des lignes
Dans chacun des 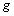 ,
, 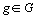 , tableaux de contingence on définit les profils-lignes
centrés,
, tableaux de contingence on définit les profils-lignes
centrés,
|
|
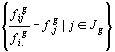
|
|
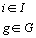
|
|
(1)
|
avec les poids 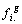 ,
, 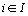 et la métrique de matrice associée la matrice diagonale des
et la métrique de matrice associée la matrice diagonale des 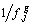 ,
, 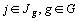 .
.
Puisque l' on cherche à
analyser ensemble les 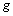 ,
, 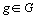 , tableaux et que les profils-lignes de chaque tableau sont
représentés dans des espaces distincts, chacun dans un espace de dimension
, tableaux et que les profils-lignes de chaque tableau sont
représentés dans des espaces distincts, chacun dans un espace de dimension 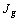 , il faut chercher un espace commun dans lequel on puisse
effectuer l' analyse. Cet espace commun est
, il faut chercher un espace commun dans lequel on puisse
effectuer l' analyse. Cet espace commun est 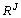 , où l' on représente les profils-lignes de chacun des tableaux,
appelés profils-lignes partiels. Les coordonnées de ces points correspondent à
celles définies en (1), en complétant le reste des coordonnées par 0. Le
profil-ligne partiel
, où l' on représente les profils-lignes de chacun des tableaux,
appelés profils-lignes partiels. Les coordonnées de ces points correspondent à
celles définies en (1), en complétant le reste des coordonnées par 0. Le
profil-ligne partiel 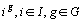 a alors pour coordonnées:
a alors pour coordonnées:
|
|
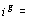 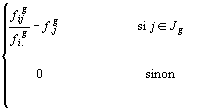
|
|
(2)
|
L' ensemble des profils-lignes partiels d' un même
tableau forment un sous-nuage de points que nous noterons 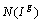 .
.
Afin d' effectuer
l' analyse conjointe, on cherche pour chaque ligne un représentant, que
nous noterons 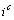 ,
, 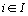 dit "compromis", qui représente le sous-nuage de
profils-lignes formé par tous les points de la même ligne dans les différents
tableaux. L' ensemble de tous les représentants sur
dit "compromis", qui représente le sous-nuage de
profils-lignes formé par tous les points de la même ligne dans les différents
tableaux. L' ensemble de tous les représentants sur 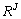 , muni de la métrique de matrice associée la matrice
diagonale des
, muni de la métrique de matrice associée la matrice
diagonale des 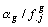 ,
, 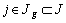 , forme le nuage
, forme le nuage 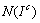 . Le compromis est choisi avec l' objectif que son
inertie puisse s' exprimer comme une somme pondérée des inerties des
profils-lignes partiels:
. Le compromis est choisi avec l' objectif que son
inertie puisse s' exprimer comme une somme pondérée des inerties des
profils-lignes partiels:
|
|
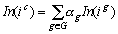
|
|
(3)
|
et que, par conséquent,
l' inertie du nuage compromis s' exprime comme somme pondérée des
inerties des nuages partiels. Pour cela on définit le compromis comme moyenne
pondérée des profils-lignes partiels 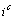 avec les poids
avec les poids 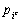 ,
, 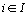 ,
,
avec 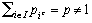 .
.
Si l' on considère 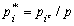 (avec
(avec 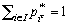 ), les résultats factoriels ne se verront altérés que dans la
proportion
), les résultats factoriels ne se verront altérés que dans la
proportion 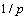 . On a considéré
. On a considéré 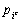 dans la mesure où cela rend les formules plus claires.
dans la mesure où cela rend les formules plus claires.
2.3 Obtention des facteurs
Afin de chercher la relation entre les analyses des lignes
et des colonnes dans les développements suivants, l' analyse factorielle
de l' ensemble des tableaux de contingence s' effectue en recherchant
les valeurs propres 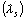 et les vecteurs propres
et les vecteurs propres 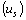 ,
, 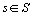 , issus de la diagonalisation de la matrice
, issus de la diagonalisation de la matrice 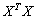 où le terme général de la matrice
où le terme général de la matrice 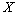 est:
est:
|
|
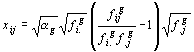
|
|
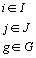
|
|
(4)
|
De plus, on utilisera les
matrices diagonales 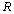 d' ordre
d' ordre 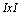 et
et 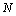 d' ordre
d' ordre 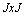 , de termes généraux respectivement:
, de termes généraux respectivement:
On définit aussi la matrice 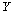 , diagonale par blocs, où chaque bloc de la diagonale est la
matrice
, diagonale par blocs, où chaque bloc de la diagonale est la
matrice 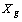 d' ordre
d' ordre 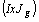 qui se compose des coordonnées de la matrice
qui se compose des coordonnées de la matrice 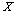 pour l' ensemble
des colonnes
pour l' ensemble
des colonnes 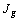 du tableau
du tableau 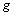 ,
, 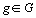 , et on définit la matrice
, et on définit la matrice 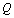 , diagonale par blocs aussi, où chaque bloc est, de même, une
matrice diagonale d' ordre
, diagonale par blocs aussi, où chaque bloc est, de même, une
matrice diagonale d' ordre 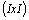 et de terme général
et de terme général 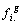 ,
, 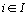 ,
, 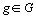 .
.
Puisque dans l' analyse des
lignes on diagonalise la matrice 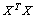 et dans celle des
colonnes la matrice
et dans celle des
colonnes la matrice 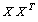 la relation entre les valeurs propres et vecteurs propres des
analyses des lignes
la relation entre les valeurs propres et vecteurs propres des
analyses des lignes 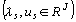 et colonnes
et colonnes 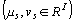 est:
est:
2.4 Projections
des profils
On calcule les projections
sur l' axe 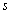 ,
, 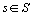 , des profils-lignes partiels
, des profils-lignes partiels 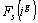 , des compromis
, des compromis 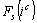 ,
, 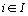 , et des profils-colonnes
, et des profils-colonnes 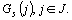 Les projections de
tous les profils-lignes partiels et compromis sont respectivement
Les projections de
tous les profils-lignes partiels et compromis sont respectivement 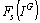 avec
avec 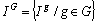 et
et 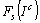 et de toutes les colonnes
et de toutes les colonnes 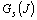 . Les projections sur l' axe
. Les projections sur l' axe 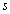 ,
, 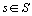 , des lignes et colonnes sont calculées en sachant
qu' il est nécessaire d' éliminer l' effet de
l' introduction des poids et les profils-lignes partiels sont projetés
comme supplémentaires en éliminant aussi l' effet de l' introduction
du poids:
, des lignes et colonnes sont calculées en sachant
qu' il est nécessaire d' éliminer l' effet de
l' introduction des poids et les profils-lignes partiels sont projetés
comme supplémentaires en éliminant aussi l' effet de l' introduction
du poids:
2.5 Aides
à l’interprétation
Dans l' analyse proposée, on peut obtenir les mêmes
aides à l' interprétation que dans les analyses factorielles habituelles.
Les contributions des points à la
formation de l' axe 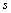 ,
, 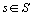 , sont calculées de la manière habituelle en divisant
l' inertie projetée d' un point (poids par coordonnée au carré) par
la somme des inerties de tous les points du nuage sur l' axe
, sont calculées de la manière habituelle en divisant
l' inertie projetée d' un point (poids par coordonnée au carré) par
la somme des inerties de tous les points du nuage sur l' axe 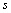 , c'est-à-dire:
, c'est-à-dire:
La qualité de représentation
d' un point sur l' axe 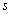 ,
, 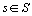 , se mesure par les contributions relatives. On les
calcule par le quotient de l' inertie projetée du point sur l' axe
, se mesure par les contributions relatives. On les
calcule par le quotient de l' inertie projetée du point sur l' axe 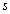 ,
, 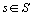 , sur l' inertie totale du point ou par le
carré de la projection sur l' axe
, sur l' inertie totale du point ou par le
carré de la projection sur l' axe 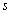 ,
, 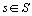 , sur la distance, au carré, du point à l' origine:
, sur la distance, au carré, du point à l' origine:
avec pour distance, au carré, de la colonne 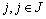 à l' origine:
à l' origine:
et pour la
distance, au carré, du compromis à l' origine:
Les relations
entre les projections des lignes (compromis) et colonnes ainsi que leurs
propriétés peuvent être consultées dans [ZAR 02] et [GOI 02].
3. Application
de l' Analyse Simultanée à l' étude d' un tableau lexical
ternaire
3.1 Les
Données
Pour l' application de
l' Analyse Simultanée à l' étude de données textuelles on a recours
aux données relatives à l' enquête qui se trouve dans la base de données
du logiciel SPAD (version 5.0), sous le nom Enq_nt.sba. Cette enquête contient
les réponses de 300 individus à 12 questions fermées, portant sur sexe, état
civil, catégories d' âge, niveaux d' études, etc. Parmi ces questions
se trouvent "Opinion sur le mariage" avec 4 modalités de réponse:
Union indissoluble, dissolution en cas grave, dissolution en cas d' accord
mutuel et la modalité ne sais pas ainsi que "Nombre idéal
d' enfants" avec 5 modalités de réponse: 0 ou 1 enfant, 2, 3, 4 ou
plus et non-réponse. Associées à ces deux dernières questions, se trouvent deux
questions ouvertes dans lesquelles on consulte les individus en les
interrogeant: pourquoi? "Pourquoi avez-vous cette opinion sur le
mariage?" et "Pourquoi ce nombre idéal d' enfants?" Dans
l' application présentée dans le cadre de ce travail, on a sélectionné la
question ouverte relative à l' opinion sur le mariage et les mots utilisés
par les personnes interrogées au moment d' y répondre. Les 300 personnes
interrogées répondent à cette question ouverte en utilisant 639 mots
différents, prononcés au total en 3419 occasions. Sur ces mots employés, on a
retenu les 84 qui apparaissent avec une plus grande fréquence que six. Lesquels
ont été prononcés au total en 2467 occasions.
Par ailleurs, en ce qui concerne
les caractéristiques des individus, on a retenu pour l' étude le sexe, les
catégories d' âge et les modalités de réponse à la question fermée
relative à l' opinion sur le mariage.
Outre les mots, utilisés comme
actifs dans l' analyse, on a sélectionné les 120 segments répétés avec une
fréquence supérieure à quatre. [LEB 88] définissent les segments comme
"toute suite d' occurrences consécutives dans le corpus et non
séparées par un séparateur de séquence". L' utilisation de ces
segments comme éléments illustratifs permet de remettre dans leur contexte les
mots isolés en améliorant l'interprétation des résultats de l'analyse.
La sélection du vocabulaire de mots
ainsi que des segments répétés a été réalisée en recourant aux méthodes
d'Analyse Textuelle de SPAD (MOTS, VOSPEC y SEGME).
Ainsi, l' Analyse Simultanée
s' applique (figure 2) aux quatre tableaux de contingence, un pour
chaque catégorie d' âge: 17-25, 26-39, 40-59, 60 ou plus, dont les lignes
sont constituées par les 84 mots retenus et dont les colonnes sont le résultat
du croisement des deux modalités de sexe et des trois d' opinion sur le
mariage (la modalité ne sais pas a été éliminée pour son faible effectif). Le
terme général de chaque tableau représente la fréquence avec laquelle le mot i
a été employé par la catégorie j.
Figure 2: Tableaux à analyser
Dans l' analyse ces dernières
modalités sont identifiées par une série de caractères. Ainsi, par exemple, 1-in17.25ho
représente le profil des mots employés par les individus du groupe 1,
d' âge compris entre 17 et 25 ans, quand ils jugent le mariage
indissoluble (in), et il s' agit d' hommes (ho).
3.2 Résultats
de l' Analyse Simultanée
Sachant que l' Analyse Simultanée
permet que chaque groupe maintienne sa propre structure interne, les relations
établies entre les différentes opinions sur le mariage (indissoluble,
dissolution en cas d'accord mutuel, dissolution en cas grave), à
l' intérieur de chaque groupe d' âge sont celles que l' on
trouverait dans chacune des quatre analyses séparés. Ceci étant,
l' Analyse Simultanée permet de réfleter les relations internes à chaque
tableau et les relations entre les différents tableaux à un seul référentiel
commun, les axes créés à partir du nuage de mots-compromis (§ 2.2).
Le premier plan factoriel résultant
de l' Analyse Simultanée des quatre tableaux représente 25.63% de
l' inertie (tableau 1).
Les trois premiers groupes
d' âge présentent une contribution similaire dans la création des deux
facteurs (tableau 2), la contribution du quatrième groupe étant la moins
importante. On considère la contribution d' un groupe à un facteur comme
la somme des contributions de ses éléments à ce facteur.
|
Inertie
|
Pourcentage
|
Pourcentage
|
|
|
|
|
cumulé
|
|
Axe 1
|
1.64
|
13.10
|
13.10
|
|
Axe 2
|
1.57
|
12.53
|
25.63
|
|
Axe 3
|
1.24
|
9.92
|
35.55
|
|
|
|
|
|
|
In Tot
|
12.54
|
|
|
Tableau
1: Inerties projetées sur les axes et Inertie totale
|
|
Axe 1
|
Axe 2
|
Axe
3
|
|
G=1 (17.25)
|
0.2627
|
0.2355
|
0.06264
|
|
G=2 (26.39)
|
0.3024
|
0.3655
|
0.12230
|
|
G=3 (40.59)
|
0.3007
|
0.2758
|
0.32487
|
|
G=4
(60+)
|
0.1342
|
0.1232
|
0.49019
|
Tableau
2: Contributions de chaque tableau à l' Analyse Simultanée
L' étude de la
multidimensionnalité des groupes se réalise à travers la mesure L(g),
comparable à celle utilisée dans l' Analyse Factorielle Multiple [ESC 84]
et [ZAR 03]. Le tableau 3 montre comment le troisième et le quatrième
groupe sont les plus multidimensionnels et, pour cette raison, ceux qui
contribuent le plus à la formation du troisième facteur.
|
g=1 (17.25)
|
2.0846
|
|
g=2 (26.39)
|
1.9903
|
|
g=3 (40.59)
|
2.6751
|
|
g=4 (60+)
|
2.2450
|
Tableau
3: L(g)
Sur le plan factoriel sont représentées les
trois opinions sur le mariage: Indissoluble, dans le second quadrant du plan
(figure 3), dont les modalités contribuent à 50.77% de l' inertie du
second facteur. Les contributions les plus fortes étant celles relatives au
groupe d' âge de 26 à 39 ans (24.5%). La dissolution d' un commun
accord, dans le troisième quadrant, occupe une partie du quatrième quadrant.
Les modalités de ce groupe d' opinion contribuent surtout à la création du
second facteur et apportent 38.69% de son inertie. Enfin, la dissolution en cas
grave se projette pratiquement au centre de gravité du second facteur et
détermine le premier facteur dans sa partie positive, en contribuant à 62.23%
de son inertie.
Dans chacune des trois options
possibles sur le mariage, les projections des profils de mots par âge et sexe
permettent de vérifier une certaine dispersion. Ce qui indique qu' en
dépit de l' existence d' un vocabulaire caractéristique pour chacune
des opinions sur le mariage, il existe, par ailleurs, à l' intérieur de
chacune d' elles un usage différent du langage selon l' âge et le
sexe. Par exemple, la séparation entre les projections des hommes de plus de 60
ans et de moins de 25 qui jugent le mariage indissoluble (4-in60.ho et
1-in17.25ho, respectivement) indique un vocabulaire différent en fonction de
l' âge. L' usage de mots différents entre hommes et femmes qui
possèdent le même âge et la même opinion sur le mariage est vérifiable, par
exemple, parmi les jeunes de 17 à 25 ans, qui considèrent valable la
dissolution en cas grave (1-gr17.25fe et 1-gr17.25ho).
Nous pouvons trouver, avec la
projection des mots-compromis (figure 4), certains mots qui sont plus spécifiques
de chacune des trois opinions et l' on peut expliquer à travers la
projection des profils partiels des mots, la dispersion mentionnée auparavant.
De même, la projection, comme éléments supplémentaires, des segments répétés
(figures 5 et 6) permet d' interpréter le contexte dans lequel
ces mots sont utilisés par les individus.
On a opté pour représenter les
projections des profils-colonnes, des mots-compromis et des segments répétés en
figures différentes, au lieu de la représentation simultanée habituelle, pour
faciliter la lecture et l' interprétation de leurs relations.
Le grand nombre de mots avec une
projection proche de l' origine n' indique rien d' autre
qu' une utilisation assez commune du langage, en général, par tous les
individus interrogés.
Parmi les mots-compromis qui
participent dans la formation des axes, ceux qui présentent les contributions
les plus fortes sont aussi majoritairement ceux qui constituent le vocabulaire
spécifique des individus, dans le sens de l' Analyse Textuelle [LEB 88],
lorsqu' ils émettent une opinion ou une autre.
L' Analyse
Simultanée montre comment les mots qui caractérisent le mieux ceux qui jugent
que le mariage est indissoluble sont les mots spécifiques, selon la méthode
"VOSPEC" de SPAD, pour cette opinion: marie, suis, avant, on,
pour, doit, trop, vie. Ces mots totalisent 30.91% de l' inertie du
second axe.
Vu que dans
cette opinion la contribution la plus forte est due aux modalités des individus
de 26 à 39 ans, les mots cités sont très associés à ce groupe d' âge.
La projection de certains segments
lexicaux (ou segments répétés) comme lignes supplémentaires
(figures 5 et 6) illustre encore plus le vocabulaire employé
par ces individus: le mariage est, on se marie, pour la vie, c' est
pour, rester ensemble, est un contrat, je suis, etc. Certains de ces mots,
séparément, n' ont pas contribué à la formation des axes. Cependant, les
segments cités montrent clairement le contexte linguistique de ceux qui jugent
le mariage indissoluble. Les segments mentionnés permettent de reconstruire
certaines des réponses de ces individus: "Si on se marie c' est
pour rester ensemble", "On se marie pour la vie" ou "C' est
pour la vie".
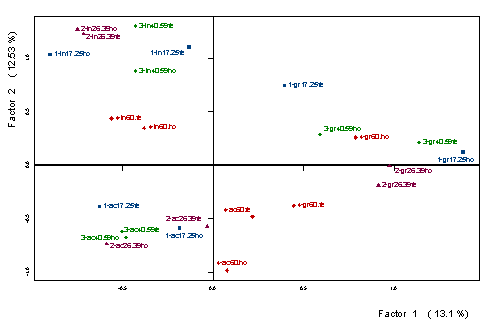 Figure
3: Projection des profils-colonnes
Figure
3: Projection des profils-colonnes
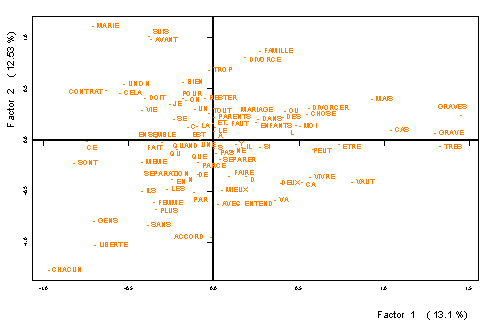 Figure 4: Projection des compromis
Figure 4: Projection des compromis
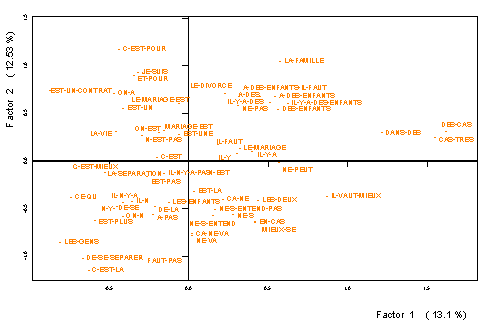 Figure
5: Projection des segments répétés (I)
Figure
5: Projection des segments répétés (I)
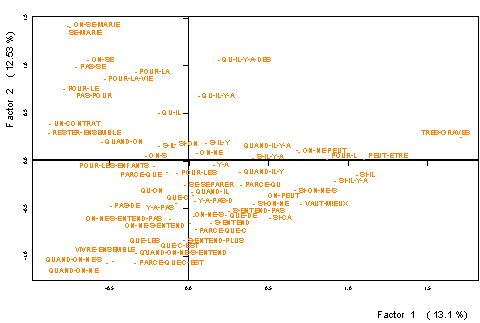 Figure
6: Projection des segments répétés (II)
Figure
6: Projection des segments répétés (II)
Les mots les plus spécifiques
employés par les individus quand ils jugent que le mariage admet la dissolution
par consentement mutuel sont: chacun, liberté, les, plus, sans, gens,
accord, entend, mieux, ce qui explique 27.81% de l' inertie du second
facteur. Parmi les segments employés par ces individus se trouvent: quand on
ne s' entend, vivre-ensemble, de se séparer, parce que c' est, faut
pas, les gens, etc. Certaines de leurs réponses caractéristiques sont: "Parce
que c' est la solution la plus intelligente quand on ne peut plus vivre
ensemble", "Parce que quand on ne s' entend, il n' y a rien
à faire de mieux que de se séparer, chacun est libre tout de même",
"C' est une question de liberté chacun doit pouvoir organiser sa vie
de la manière la plus souhaitable", "Si les époux ne
s' entendent pas c' est mieux de se séparer d' accord plutôt que
de se gacher la vie à deux" et celles qui font référence à la liberté:
"Liberté", "Liberté individuelle", "Entière
liberté".
Quand les individus jugent possible
la dissolution du mariage en cas grave, ils emploient un vocabulaire plus
spécifique concrétisé par des mots comme: cas, très, grave, graves, peut,
mais, ça, vaut, des, être, qui totalisent 53.54% de l' inertie du
premier facteur et les segments les plus répétés sont: il vaut mieux, dans
des, des cas, des enfants, cas très, très graves, si il y a, peut être, on ne
peut, etc. qui caractérisent des opinions indiquant que le mariage ne doit
dissoudre que dans les cas graves: "Tout est revisable. On peut
toujours améliorer la situation familiale sauf bien sur cas très graves
(adultère)"; notamment quand il existe des enfants: "Si
il y a des enfants, c' est très grave de divorcer", "Surtout si
il y a des enfants".
De plus, on observe comment les
mots ce et sont contribuent à la création du premier facteur,
indiquant par là des mots peu utilisés par ceux qui admettent la dissolution du
mariage uniquement en cas grave.
Comme on l' a dit, il existe
un vocabulaire commun à certains groupes d' âge et de sexe indépendamment
de leur opinion sur le mariage. On a aussi des mots qui, bien qu' ils
caractérisent plus l' une des opinions, font également partie des réponses
des deux autres opinions. Tout cela implique que l' on projette des
colonnes éloignées de leurs homologues. Ainsi, par exemple, on observe comment
le vocabulaire des femmes de 17-25 ans qui jugent possible la dissolution du
mariage en cas grave (1-gr17-25fe) se situe dans le premier quadrant du plan
factoriel à mi-chemin entre le vocabulaire employé par ceux qui jugent
qu' il est indissoluble et ceux qui admettent la dissolution en cas grave.
C' est-à-dire que ces personnes partagent du vocabulaire avec
l' opinion d' indissolubilité. Ainsi en va-t-il de mots comme famille,
marie, suis, union, tout. De manière analogue on apprécie comment les
individus de plus de 60 ans, quand ils jugent que le mariage est indissoluble
(4-in60fe et 4-in60ho), utilisent un vocabulaire partagé avec les personnes
interrogées qui admettent la dissolution en cas d' accord mutuel ou en cas
grave. C' est le cas de mots comme enfants, est, faut, pas, etc.
La projection des profils-lignes
partiels permet d' observer la dispersion des mots émis par chaque groupe
d' âge par rapport à la projection du mot-compromis correspondant. Ainsi,
on peut observer comment les mots caractéristiques employés dans une opinion
concrète présentent une faible dispersion par rapport au compromis. Il en va
ainsi, par exemple, des chacun, liberté, sans et gens (figure 7),
mots utilisés presque exclusivement par les individus qui jugent possible la
dissolution du mariage en cas de consentement mutuel. Dans cette figure on
observe de plus comment chacun est utilisé uniquement par les individus
entre 26 et 59 ans (les projections de 1chacun et 4chacun se
trouvent à l' origine) et comment les individus âgés de plus de 60 ans
n' emploient pas les termes liberté, sans et gens.
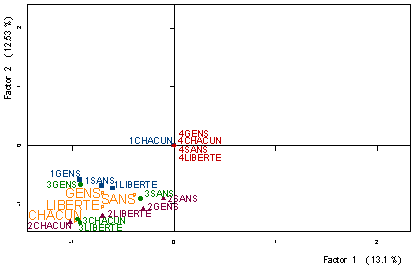
Figure 7: Projection des profils-lignes partiels (I)
Sur les plans les profils partiels
sont identifiés par le mot précédé du numéro qui indique le tableau (groupe
d' âge) auquel il appartient.
La projection des profils-lignes
partiels permet de plus d' observer des mots qui sans être considérés
caractéristiques, du fait d' une faible contribution, sont, néanmoins,
davantage associés à l' une des opinions.
C' est le cas de mots comme cela,
contrat, bien (figure 8) plus associés à l' opinion Indissoluble,
quoique bien, par exemple, soit également utilisée par les plus jeunes
quand ils jugent que le mariage peut être dissous en cas grave.
Des mots comme avec, ensemble,
femme, quand, même, séparation (figure 9) sont plus associés à la
possibilité de dissolution par consentement mutuel, même si, par exemple, ensemble
est également utilisée par les individus de 26 à 39 ans quand ils jugent que le
mariage est indissoluble et bien que les personnes de plus de 60 ans emploient femme
et même quand ils jugent respectivement que le mariage admet la
dissolution en cas grave ou qu' il est indissoluble.
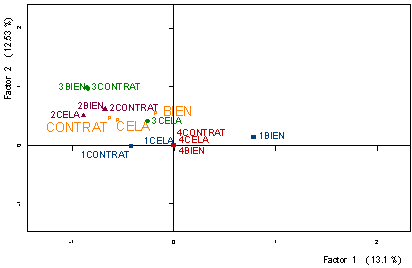 Figure
8: Projection des profils-lignes partiels (II)
Figure
8: Projection des profils-lignes partiels (II)
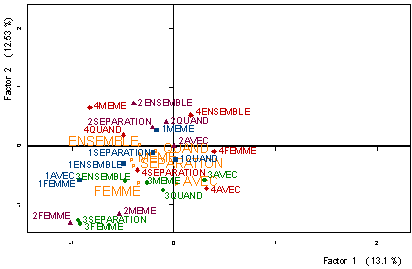
Figure 9: Projection des profils-lignes partiels (III)
Plus associés à
l' opinion de dissolution en cas grave se trouvent enfants, dans, moi,
divorcer, vivre (figure 10), quoique à nouveau certains d' entre
eux également sont employés quand ils croient le mariage indissoluble; tel est
le cas de enfants utilisé par les individus de plus de 60 ans.
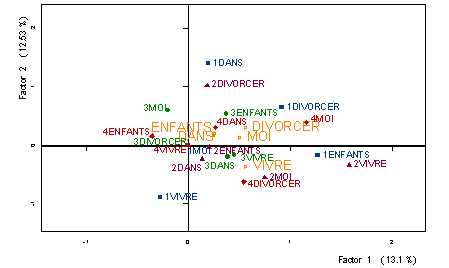
Figure 10: Projection des profils-lignes partiels (IV)
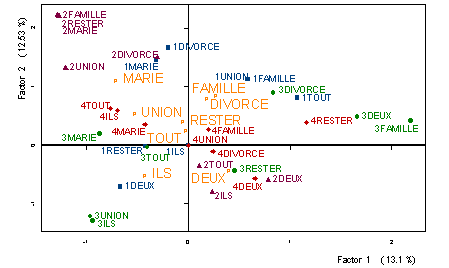
Figure 11: Projection des profils-lignes partiels (V)
Enfin, la
considération des profils-lignes partiels permet de détecter l' existence
de mots ayant une grande dispersion par rapport à leur compromis pour avoir été
utilisés par les individus de différents groupes d' âge et de différentes
opinions. C' est le cas de mots comme deux, divorce, divorcer, famille,
ils, parents, rester, tout, union (figure 11). Rester, par
exemple, est employé par les individus de 26 à 39 ans dans le cas de mariage
indissoluble; par ceux de plus de 60 ans quand ils jugent que l' on peut
dissoudre en cas grave et par ceux de 40 à 59 ans quand ils jugent que le
mariage admet la dissolution, dans les deux cas envisagés dans l' enquête.
Jusqu' ici, on a commenté
principalement les aspects concrets du vocabulaire spécifique employé par les
personnes interrogées dans chacune des opinions sur le mariage. L' Analyse
Simultanée permet aussi d' observer un autre type de différences dans
l' utilisation du langage, comme ce peut être le cas dans le temps verbal,
dans l' utilisation des pluriels ou dans l' emploi différent
d' un même mot.
Par exemple, il semble qu' en
général l' emploi des verbes à l' infinitif (divorcer, vivre,
séparer, être) est plus fréquent quand il s' agit de la dissolution en
cas grave que dans les deux autres cas.
De plus, on observe parmi les
individus qui jugent que le mariage est dissoluble, soit qu' il le soit
seulement en cas grave soit par consentement mutuel, un usage plus important
des pluriels (ils, les, des, deux, sont) par rapport aux personnes
interrogées qui n' acceptent pas la dissolution du mariage, lesquels usent
en priorité du singulier dans leur vocabulaire.
On relèvera également que parmi les
individus qui jugent que le mariage peut être dissous, ceux qui sont favorables
au consentement mutuel emploient davantage l' adverbe quand: quand on
ne s' , quand on ne, quand on ne s' entend, etc., dans les
réponses à la question ouverte étudiée, tandis que ceux qui admettent la
dissolution en cas grave emploient plus fréquemment le conditionnel si: si
il y a, si on ne s' , si on ne, etc.
La projection des segments répétés
permet également de vérifier le contexte différent dans lequel un mot peut être
employé selon l' opinion. Il existe des mots avec une projection centrale
dans le plan et sans contribution à celui-ci, qui prennent de
l' importance avec les projections des segments répétés. C' est ce qui
se passe, par exemple, avec des mots qui indiquent un vocabulaire en termes
négatifs comme n' , ne, pas. En dépit d' être fréquents dans
toutes les opinions, ils sont plus utilisés par les individus favorables à la
dissolution du mariage (en cas grave ou accord mutuel). Ceci se vérifie avec
les projections des segments répétés dans lesquels apparaissent: quand on
ne, on ne peut, on ne s' entend pas,... En revanche, ceux qui ne
croient pas à la dissolution du mariage emploient un vocabulaire en termes
positifs.
Plus caractéristique de
l' importance du contexte est le cas de ensemble. Ce mot se
projette sur le centre de gravité du second axe mais les segments répétés: rester
ensemble et vivre ensemble, ont des positions caractéristiques;
tandis que le premier est utilisé par ceux qui jugent que le mariage est
indissoluble le second est utilisé par ceux qui se montrent partisans
d' une dissolution en cas d'accord mutuel.
Cette différence dans
l' emploi de ensemble liée à l' utilisation ou l' absence
des termes négatifs confirme le sens des réponses de ceux qui acceptent la
dissolution: "C' est pas une vie quand on ne s' entend pas de
vivre ensemble", "Tout a fait normal de se séparer si on ne
s' entend plus ensemble" et de ceux qui croient à
l' indissolubilité du mariage "On se marie pour rester
ensemble", "Pour le meilleur et pour le pire on doit rester
ensemble".
Le mot enfants est également
employé dans des contextes linguistiques différents. Les personnes interrogées
favorables à la dissolution en cas d' accord font référence à les
enfants: "Parce que c' est mieux pour les enfants",
"Pour eviter de faire souffrir les enfants"; alors que le reste
justifient leur position en fonction de l' existence d' enfants, il
y a des enfants: "Si il y a des enfants, c' est très grave de
divorcer" (diss. cas grave), "Si il y a des enfants surtout,
c' est trop grave" (indissoluble), "S' il y a des
enfants et dans tous les cas on ne peut pas se séparer"
(indissoluble).
4. Conclusions
L' Analyse Simultanée
présentée complète la méthodologie classique existante pour le traitement
d' un ensemble de tableaux de contingence. Tableaux qui peuvent provenir
ou non d' un tableau ternaire, puisqu' elle permet que les colonnes
des tableaux soient différentes.
L' Analyse Simultanée permet
de maintenir dans un étude conjointe les relations internes à l' intérieur
de chaque tableau. Elle devient utile, en particulier, quand il existe des
différences dans les totaux, dans les marges-en-ligne ou dans l' intensité
de structure entre les tableaux.
L' Analyse Simultanée admet, par ailleurs, l’introduction
simultanée de questions ouvertes et fermées ainsi que la possibilité d’analyser
conjointement des tableaux de variables de différente nature (continues,
qualitatives, de fréquence).
L' Analyse Simultanée permet de compléter l’étude conjointe de
tous les tableaux avec une comparaison globale des ceux-ci, en facilitant l’interprétation des
ressemblances et des différences entre les tableaux analysés.
L' application présentée
permet de confirmer l' utilité de la méthode dans l' analyse de
données textuelles.
L' Analyse Simultanée indique qu' en dépit de
l' existence d' un vocabulaire caractéristique pour chacune des
opinions sur le mariage, il existe, par ailleurs, à l' intérieur de
chacune d' elles un usage différent du langage selon l' âge et le
sexe.
L' Analyse Simultanée montre comment les mots qui
caractérisent le mieux ceux qui jugent que le mariage est indissoluble sont les
mots spécifiques: marie, suis, avant, on, pour, doit, trop, vie et
certains segments lexicaux comme: le mariage est, on se marie, pour la vie,
c' est pour, rester ensemble, est un contrat, je suis, etc.
Les mots les plus spécifiques employés par les individus
quand ils jugent que le mariage admet la dissolution par consentement mutuel
sont: chacun, liberté, les, plus, sans, gens, accord, entend, mieux.
Parmi les segments employés par ces individus se trouvent: quand on ne
s' entend, vivre-ensemble, de se séparer, parce que c' est, faut pas,
les gens, etc.
Quand les individus jugent possible la dissolution du
mariage en cas grave, ils emploient un vocabulaire plus spécifique concrétisé
par des mots comme: cas, très, grave, graves, peut, mais, ça, vaut, des,
être et les segments les plus répétés sont: il vaut mieux, dans des, des
cas, des enfants, cas très, très graves, si il y a, peut être, on ne peut, etc.
La projection des profils-lignes partiels permet
d' observer la dispersion des mots émis par chaque groupe d' âge par
rapport à la projection du mot-compromis correspondant; permet de plus
d' observer des mots qui sans être considérés caractéristiques sont,
néanmoins, davantage associés à l' une des opinions et, enfin, permet de
détecter l' existence de mots ayant une grande dispersion par rapport à
leur compromis pour avoir été utilisés par les individus de différents groupes
d' âge et de différentes opinions.
L' Analyse Simultanée permet
aussi d' observer un autre type de différences dans l' utilisation du
langage, comme ce peut être le cas dans le temps verbal, dans
l' utilisation des pluriels ou dans l' emploi différent d' un
même mot.
Remerciements
Ce travail a été financé par le projet d' investigation
UPV 038.321-HA041/99 de l' Université du Pays Basque (UPV/EHU) et UPV
00038.321-13631/2001 et le projet PB98-0149 de la Direction Génerale de
l' Enseignement supérieur et de la Recherche Scientifique du Ministère
Espagnol de l' Éducation et de la Culture
Références
[BEC 99] BÉCUE-BERTAUT, Mónica. & PAGÈS, Jérôme.,
Intra-sets multiple factor analysis. Application to textual data. In J.Jansen et al., editors, Proc.
of ASMDA’99 (9th International Symposium on Applied Stochastic
Models and Data Analysis) pp,51-60, 1999
[BEC 00 a] BÉCUE-BERTAUT, Mónica. & LEBART,
Ludovic., Analyse statistique de réponses ouvertes : application à des
enquêtes auprès de lycéens, in L’Analyse des correspondances et les
techniques connexes. Approches nouvelles pour l’analyse statistique des
données, J. Moreau, P.A. Doudin, P. Cazes Ed. pp,60-83, 2000
[BEC 00 b] BÉCUE-BERTAUT, Mónica. & PAGÈS, Jérôme.,
Analyse factorielle multiple intra-tableaux. Application à l’analyse simultanée
de plusieurs questions ouvertes., in ‘JADT 2000: 5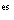 Journées Internationales d’Analyse Statistique des Données
Textuelles´, 2000
Journées Internationales d’Analyse Statistique des Données
Textuelles´, 2000
[BEC 02] BÉCUE-BERTAUT, Mónica. & PAGÈS, Jérôme.,
Analyse conjointe de questions ouvertes et de questions fermées :
méthodologie, exemple., in ‘JADT 2000: 6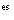 Journées Internationales d’Analyse Statistique des Données
Textuelles´, 2002
Journées Internationales d’Analyse Statistique des Données
Textuelles´, 2002
[ESC 84] ESCOFIER, Brigitte & PAGÈS, Jérôme., L’Analyse
Factorielle Multiple, Cahiers du Bureau Universitaire de Recherche
Opérationnelle, 42, pp,1-48, 1984
[ESC 88] ESCOFIER, Brigitte & PAGÈS, Jérôme., Analyses
Factorielles Simples et Multiples. Objetifs, méthodes et interprétation, DUNOD,
1988
[GOI 02] GOITISOLO, Beatriz., El Análisis Simultáneo.
Propuesta y Aplicación de un nuevo método de análisis factorial de tablas de
contingencia, Tesis Doctoral, Universidad del País Vasco, Bilbao, 2002
[LEB 88] LEBART, Ludovic & SALEM, Andre., Analyse
Statistique des Données Textuelles, DUNOD, 1988
[LEB 94] LEBART, Ludovic & SALEM, Andre., Statistique
Textuelle, DUNOD, 1994
[LEB 98]
LEBART, Ludovic & SALEM, Andre. & BERRY, L., Exploring Textual Data, Kuwer Academic Publishers,
1998
[LHE 76] L’HERMIER DES PLANTES, H., STATIS :
Structuration de Tableaux à Trois Indices de la Statistique, Thèse (3c),
USTL, Montpellier, 1976
[ZAR 02] ZÁRRAGA, Amaya & GOITISOLO, Beatriz., Méthode
fatorielle pour l’analyse simultanée de tableaux de contingence, Revue de
Statistique Appliquée L(2), pp,47-70, 2002
[ZAR 03] ZÁRRAGA, Amaya & GOITISOLO, Beatriz., Étude de
la structure inter-tableaux à travers l’ Analyse Simultanée, Revue de Statistique Appliquée, LI(3),
pp,39-60, 2003